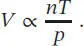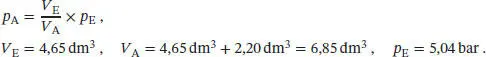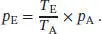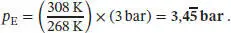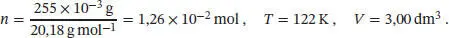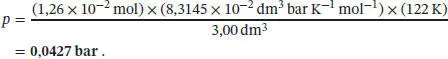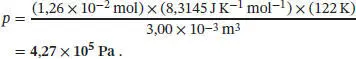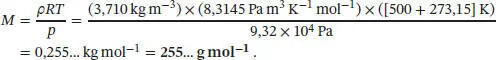James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

D1.1.1Eine Zustandsgleichung verknüpft die verschiedenen Variablen miteinander, die den Zustand eines Systems definieren. Boyle, Charles und Avogadro konnten nach entsprechenden Experimenten Gleichungen für Gase bei niedrigen Drücken (ideale Gase) herleiten. Boyle bestimmte, wie sich das Volumen mit dem Druck verändert ( V ∝ 1 / p ), Charles untersuchte den Zusammenhang von Volumen und Temperatur ( V ∝ T ), und Avogadro gab an, wie sich das Volumen mit der Menge des Gases ändert ( V ∝ n ). Wenn wir diese Proportionalitäten zu einer einzigen Gleichung zusammenfassen, erhalten wir

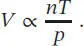
Wenn wir nun eine Proportionalitätskonstante R einführen, gelangen wir zur Zustandsgleichung des idealen Gases:

L1.1.1aMithilfe entsprechender Umrechnungsfaktoren können wir den Druck in unterschiedlichen Einheiten angeben. Es gilt: 1 atm = 101,325 kPa = 760 Torr; 1 bar entspricht exakt 10 5Pa.

1 (i) Ein Druck von 108 kPa lässt sich wie folgt in Torr umrechnen:

2 (ii) Ein Druck von 0,975 bar entspricht 0,975 × 105 Pa und lässt sich wie folgt in atm umrechnen:

L1.1.2a

1 (i) Nach der Zustandsgleichung des idealen Gases ( Gl. (1.4)) gilt pV = nRT. Auflösen nach dem Druck ergibt p = nRT/V. Die Stoffmenge n von Xenon finden wir, indem wir die im beschriebenen Experiment eingesetzte Masse durch die Molmasse dieses Gases teilen (M(Xe) = 131,29 g mol−1). Für den Druck p ergibt sichDie Probe hätte als ideales Gas folglich einen Druck von 24,4 atm anstelle von 20 atm. Die Antwort auf die Fragestellung ist daher: nein.

2 (ii) Die Van-der-Waals-Gleichung (Gl. (1.27a)) für den Druck des Gases lautetAus Tab. 1.6 im Anhang des Lehrbuchs entnehmen wir für Xenon die folgenden Van-der-Waals-Parameter: a = 4,137 dm6 atm mol−2 und b = 5,16 × 10−2 dm3 mol−1. Einsetzen dieser Konstanten ergibt folgende Terme in der Gleichung für den Druck p:Also ist .

L1.1.3aDa die Temperatur bei einer isothermen Kompression konstant gehalten wird, können wir das Boyle’sche Gesetz ( Gl. (1.3a), pV = konst.) anwenden. Das Produkt p E V E= p A V Akönnen wir nach dem Anfangs- bzw. dem Enddruck auflösen:

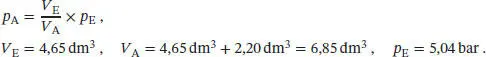
1 (i) Daraus folgt für den Anfangsdruck

2 (ii) Wegen 1 atm = 1,013 25 bar folgt weiter

L1.1.4aDie Zustandsgleichung idealer Gase, pV = nRT ( Gl. (1.4)), lässt sich für konstante Stoffmenge n und konstantes Volumen V in die Form p / T = nR / V = konst. bringen. Der Druck steigt proportional mit der Temperatur an, p ∝ T . Daraus folgt p E/ T E= p A/ T Aoder, durch Auflösen nach p E,

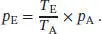
Der Reifendruck ist p A= 3 bar, die Temperaturen sind T A= −5 °C bzw. 268 K und T E= 35 °C bzw. 308 K. Damit ergibt sich durch Einsetzen

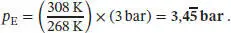
Komplikationen ergeben sich aus den Faktoren, die die Konstanz von V oder n aufheben, beispielsweise eine Änderung des Reifenvolumens oder der Elastizität des Gummis oder ein Druckverlust aufgrund eines Lecks oder durch Diffusion, der den Reifendruck verringert.

L1.1.5aWir verwenden die Zustandsgleichung idealer Gase, ( Gl. (1.4)), in der Form p = nRT/V . Gegeben sind T und V , die Stoffmenge n muss berechnet werden:

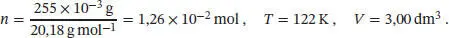
Durch Einsetzen erhalten wir für den Druck

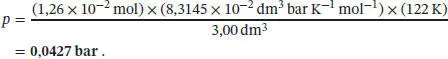
Beachten Sie, dass bei dieser Berechnung diejenige Variante der Gaskonstante R verwendet wurde, deren Einheiten den Angaben der übrigen Größen entsprechen. Alternativ könnten wir beispielsweise auch R = 8,3154 J K −1mol −1verwenden und die übrigen Einheiten entsprechend umrechnen, wodurch wir den Druck z. B. in der Einheit Pascal (Pa) erhalten:

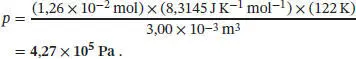
Dabei haben wir 1 dm 3= 10 −3m 3sowie 1 J = 1 kg m 2s −2und 1 Pa = 1 kg m −1s −2verwendet.

L1.1.6aWir betrachten den Schwefeldampf näherungsweise als ideales Gas und verwenden daher die Zustandsgleichung des idealen Gases ( Gl. (1.4), pV = nRT ). Unsere Aufgabe besteht zunächst darin, mithilfe dieser Gleichung einen Ausdruck für den Zusammenhang zwischen der Dichte ρ und der Molmasse M zu finden.

Zunächst führen wir über die Stoffmenge n = m / M die Molmasse M in die Zustandsgleichung des idealen Gases ein, pV = ( m/M ) RT . Division durch das Volumen V auf beiden Seiten dieser Gleichung liefert p = ( m / V )( RT / M ). Die Größe ( m / V ) entspricht der Dichte ρ , also gilt p = ρRT/M , was sich umstellen lässt zu M = ρRT/p ; dies ist die gesuchte Beziehung zwischen der Molmasse und der Dichte.

Einsetzen der Werte ergibt

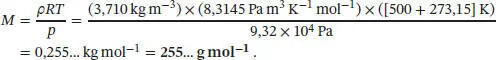
Dabei haben wir 1 J = 1 kg m 2s −2und 1 Pa = 1 kg m −1s −2verwendet. Die molare Masse von atomarem Schwefel ist 32,06 g mol −1; daher finden wir für die Anzahl N der Schwefelatome, aus denen der Schwefeldampf zusammengesetzt ist,

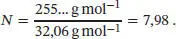
Als Ergebnis erwarten wir allerdings eine ganze, natürliche Zahl; die chemische Formel des Schwefeldampfs ist also S8.

L1.1.7aWir betrachten den Wasserdampf näherungsweise als ideales Gas und verwenden daher die Zustandsgleichung des idealen Gases ( Gl. (1.4), pV = nRT ). Unsere Aufgabe besteht zunächst darin, mithilfe dieser Gleichung einen Ausdruck für den Zusammenhang zwischen den gegebenen Werten und der Masse m zu finden.