M. Kemal Ozgoren - Kinematics of General Spatial Mechanical Systems

(3.9)

(3.10)

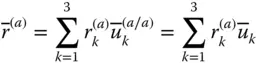
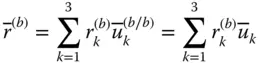
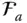Consider two reference frames and 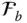. If they are differently oriented with respect to each other, a vector 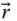appears differently in 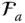and 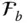. In other words, 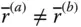. However, since 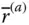and 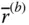represent the same vector 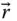, they are nonetheless related so that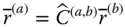

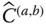(3.11)

In Eq. (3.11), is defined as the transformation matrix between 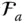and 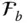. It can be considered as an operator that transforms the components of a vector from 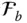to 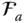. So, to be more specific, it may also be called a component transformation matrix .

1 (a) Inversion Property

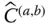Equation (3.11)can also be written in the following two ways: first by inverting ; and then by interchanging the frame indicators a and b .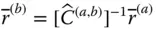

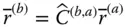
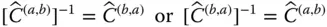
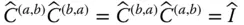
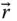(3.12)

(3.13)

Equations (3.11)– (3.13)imply the following equalities.

(3.14)

(3.15)

1 (b) Orthonormality Property

As also mentioned in Chapter 1, all the reference frames considered in this book are assumed to be orthonormal, right‐handed, and equally scaled on their axes. Therefore, the magnitude of a vector appears to be the same in every reference frame. This fact is expressed as follows: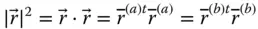

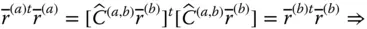
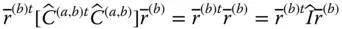
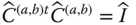
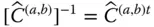
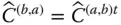
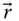(3.16)

After substituting Eq. (3.11), Eq. (3.16)can be manipulated as shown below.

(3.17)

Equation (3.17)implies the following successive equations.

(3.18)

(3.19)

Furthermore, when Eqs. (3.19)and (3.14)are compared, it is seen that

(3.20)

As seen above, the inverse of a transformation matrix is equal to its transpose. This property makes a transformation matrix an element of the set of orthonormal matrices just like a rotation matrix. The orthonormality of a rotation matrix was shown in Chapter 2.

1 (c) Combination Property

If a vector is observed in three differently oriented reference frames, such as 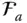, , 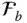and 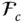, the following equations can be written to relate its column matrix representations.

(3.21)

(3.22)