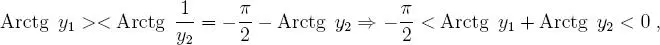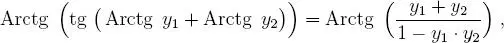Gonzalo Masjuán - Trigonometría y geometría analítica
Здесь есть возможность читать онлайн «Gonzalo Masjuán - Trigonometría y geometría analítica» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на испанском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Trigonometría y geometría analítica
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Trigonometría y geometría analítica: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Trigonometría y geometría analítica»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
integrar en un solo volumen la trigonometría, la geometría analítica, el álgebra vectorial y los números complejos, de modo que en conjunto permitan desarrollar una adecuada intuición geométrica y abordar la resolución de los diversos problemas que estas áreas consideran. La concepción pedagógica del texto permite presentar el tema como una geometría esencialmente formativa, pero también realista y utilitaria, abierta a otras áreas del conocimiento. Está dirigida a alumnos de la más diversa capacidad.

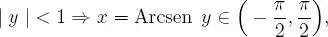
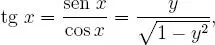
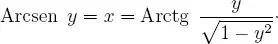
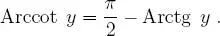
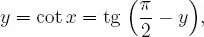 pero:
pero: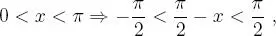
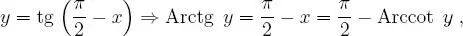
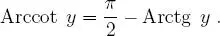
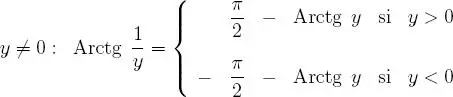
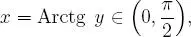 y, en consecuencia:
y, en consecuencia: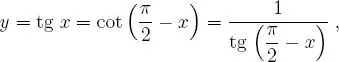
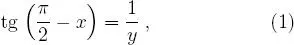
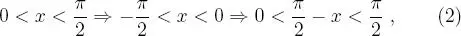
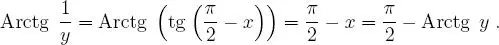
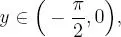 y, en consecuencia:
y, en consecuencia: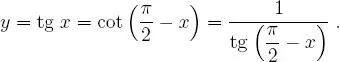
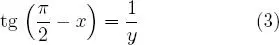
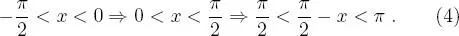
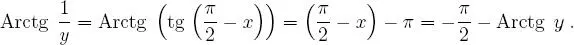
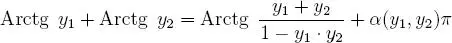
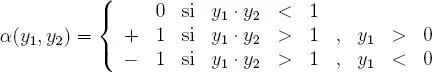
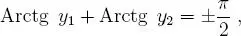
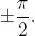
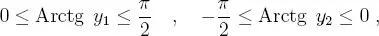
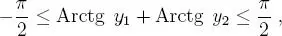
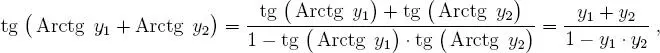
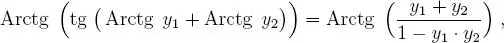
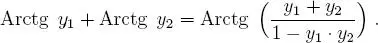
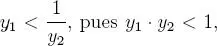 de esto se desprende que:
de esto se desprende que: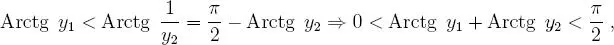
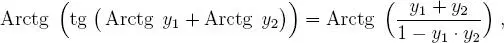
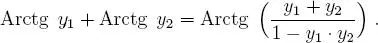
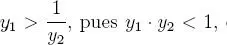 de esto se desprende que:
de esto se desprende que: