Asdrúbal Valencia Giraldo - Ciencia de los metales

La función de onda atraviesa una barrera de potencial en un pozo de potencial finito.

Es importante notar que las formas de las ondas del pozo de potencial infinito (véase figura 2.9) se deben modificar para tener en cuenta la pequeña penetración de ψ en la región de potencial más elevado: las soluciones son como se muestra en la figura 2.13. La solución que corresponde a la energía menor es la que posee la curvatura menor o la que tiene menos nodos; el primer estado excitado tendrá un nodo, el segundo dos, etc. A medida que V0 aumenta, la penetración es menor, y para V0 = ∞, se vuelve al resultado de las paredes infinitas.

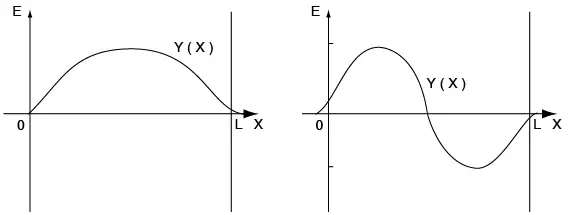
Figura 2.13 Dos soluciones de la función de onda en un pozo de potencial

A la derecha (a), solución para n=1; a la izquierda (b), solución para n=2

Las soluciones, que son simples funciones sinusoidales y exponenciales de x, solo se pueden escribir cuando V es constante en una zona. Para funciones más complicadas, las soluciones son más difíciles.

Cuando se usa el modelo de pozo de potencial para un metal, la longitud L es relativamente grande. En este caso, los electrones ocupan niveles de elevado n y los pequeños cambios respecto a las soluciones infinitas afectan principalmente la última longitud de onda, así que su efecto es despreciable (véase figura 2.14). Por consiguiente, para los casos prácticos en metales, a menos que se considere la superficie misma, el pozo de potencial infinito es un buen modelo.

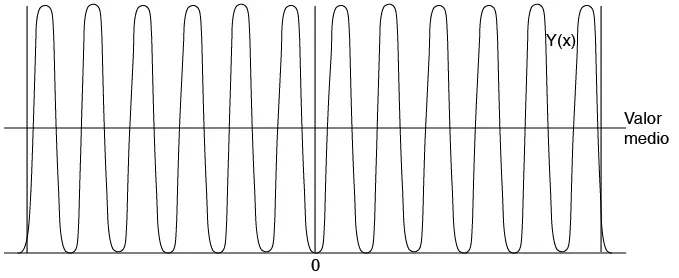
Figura 2.14 Solución de alta energía para un pozo de potencial finito

2.2.5. Números cuánticos (estructura del átomo)

En forma elemental, el modelo de un átomo aislado es el de un núcleo central, constituido por neutrones y protones, rodeado por una nube de electrones; de este modo, el átomo es eléctricamente neutro.2

A principios del siglo xx, el fisicoquímico neozelandés Ernest Rutherford estableció que el núcleo cargado positivamente tenía unas dimensiones de unos 10–14 m, y estaba rodeado por los electrones, que ocupaban una zona de unos 10–10 m alrededor de él. Niels Bohr y Arnold Sommerfeld aplicaron la teoría cuántica al modelo de Rutherford y muchos de sus postulados esenciales son válidos todavía, aunque en general su modelo fue superado por el de la mecánica ondulatoria, que es el que se considera aquí.

El átomo de H constituye la estructura más simple, pues solo contiene un electrón que se mueve en el campo de fuerza de su núcleo. En este caso, la energía potencial de la ecuación de Schrödinger está dada por la ley de Coulomb:

V(r) = –Z2/r, (2.15)

donde –Z es la carga del núcleo. Para el H, Z = 1; pero se mantiene a Z para que los resultados sean válidos si Z > 1.

Si la ecuación 2.14 se reemplaza en la ecuación 2.15, se tiene la ecuación de Schrödinger para el electrón. Esta complicación aparentemente insignificante, comparada con la del pozo de potencial, presenta, sin embargo, algunas complejidades matemáticas que no se exponen aquí; por tanto, se tratan solo las peculiaridades básicas de la solución y su significado físico.

En este tipo de problemas es conveniente considerar el movimiento del electrón en coordenadas esféricas, el centro de las cuales coincide con el núcleo del átomo (véase figura 2.15). Las coordenadas cartesianas se transforman en esféricas con las relaciones conocidas:

x = rsenθcosϕ, y = rsenθsenϕ, z = rcosθ.

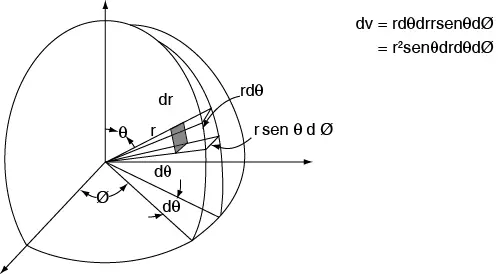
Figura 2.15 Elemento de volumen de coordenadas polares

Con la respuesta del problema de la caja tridimensional, en este caso la solución se presenta como el producto de tres funciones, cada una de las cuales solo contiene una variable,

ψ (r, θ, ϕ) = R(r)ϕ(ϕ)θ(θ).

La función R(r) describe la manera como la función de onda varía con la distancia radial r al centro del núcleo; se le denomina función radial. El producto ϕ(ϕ)θ(θ) describe la manera como varía la función de onda en diferentes direcciones del núcleo y se le llama función angular.

Como se trata de una función tridimensional, sus nodos generalmente serán superficiales (sitios donde ψ = 0). Los nodos son esféricos (en la función R), planos (en la función ϕ) y cónicos (en la función θ). Cuanto mayor sea el número de nodos en la función de onda de un electrón, se sabe que mayor es su energía.

La presencia de tres grados de libertad hace que en la solución aparezcan tres valores que solo pueden ser enteros, es decir, tres números cuánticos que se denominan n, l y m. Estos valores están presentes tanto en la componente radial como en la angular de la función de onda.

En su forma más general, la solución de la ecuación de Schrödinger para el átomo de H es:

R(r) = f1 (n, l)

θ(θ) = f2 (l, m)

ϕ(ϕ) = f3 (m).

Los números cuánticos n y l entran en la expresión de la función R o sea que determinan la función de distribución radial de la probabilidad de encontrar un electrón en un átomo. Estas funciones para el átomo de H se muestran en la figura 2.16.

En la figura 2.16, en las ordenadas se grafica R2(r) multiplicada por 4πr2. Estos valores caracterizan la probabilidad de encontrar el electrón en una cáscara esférica delgada de radio r y espesor dr; esta probabilidad es proporcional a 4πr2R2(r)dr.

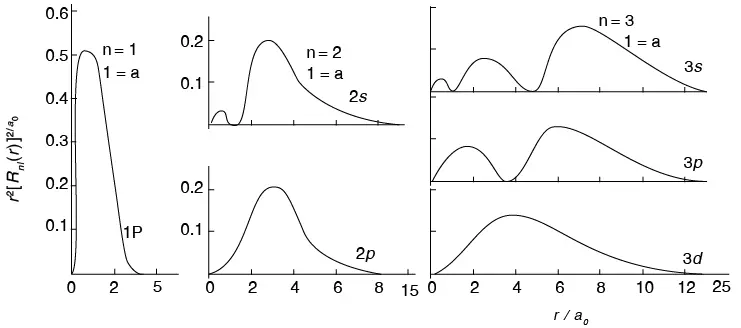
Figura 2.16 Distribución radial de la probabilidad de encontrar un electrón para diferentes estados energéticos del átomo de H

De lo anterior se comprende que, en un átomo, el electrón se podrá observar con mayor frecuencia en ciertos lugares que en otros; por esto se habla de una nube electrónica, cuya densidad estará determinada en cada punto por la probabilidad de hallar el electrón ahí. Por eso no se habla de órbita, sino de orbital, es decir, la configuración particular trazada por un electrón en un átomo. Cada orbital corresponde a una función de onda definida ψ.

Los números n, l y m determinan la configuración geométrica de la nube electrónica. También están asociados con las características físicas del movimiento del electrón.

El número cuántico n es igual al número de superficies nodales del orbital. En un nodo, ψ = 0 y ψ2 = 0 y, por tanto, la densidad de la nube electrónica es cero en un nodo. Una superficie infinitamente lejos del centro (r = ∞) también es nodal, pues en este caso ψ siempre es cero.

Así, n es el número cuántico principal y sus valores son 1, 2, 3... ∞.

Las superficies nodales, como ya se anotó, son de dos clases: las que pasan por el núcleo y las que no. Las primeras son planos o conos que atraviesan el centro; las segundas son esféricas y concéntricas. La presencia de nodos esféricos se ve en la función radial (véase figura 2.16), pues en ciertas distancias del núcleo se hace cero. El estado base o de energía mínima se da cuando r = ∞, ψ = 0 y n = 1; el siguiente estado es n = 2 y un nodo entre r = 0 y r = ∞, etc.

El valor del número cuántico l indica cuántos nodos de la función de onda pasan por el núcleo. Como uno de los nodos siempre se da cuando r = ∞, es evidente que l puede variar entre 0 y n – 1; esto es: