Fuente: Wikipedia (s. f. 6).
En la mecánica, la ecuación de una onda estacionaria (que no cambia con el tiempo) se representa por una ecuación del tipo
y = A sen(kx ± ωt),
donde y = desplazamiento, A = amplitud, x = distancia viajada, t = tiempo, k = número de onda y ω = frecuencia.
Si, admitiendo su regularidad sinusoidal, se tienen dos ondas de igual magnitud y frecuencia que viajan en direcciones opuestas a la misma velocidad, representadas por:
y1 = Asen (kx – ωt),
y2 = Asen (kx + ωt);
la onda resultante es
y = y1 + y2
y = Asen (kx – ωt) + Asen (kx + ωt)
y = 2Asenkx cosωt,
cuya forma general es la que se muestra en la figura 2.8.

Figura 2.8 La onda estacionaria y = 2Asenkx cosωt
Los puntos donde ν = 0 se llaman nodos. En los otros puntos, el desplazamiento está dado por el factor cosωt. El factor espacial 2Asenkx indica el perfil de la onda en un momento dado y el factor tiempo determina la escala. La periodicidad espacial es
λ = 2π/k,
o sea que la posición de los nodos está dada por:
x = 0, λ/2, λ, ... (n – 1)λ/2, donde n = 1, 2, 3...
En una dimensión, la ecuación diferencial de esta onda es:

y como k = 2π/λ,
 (2.2)
(2.2)
Schrödinger se valió de la relación 2.2 para escribir la ecuación de las ondas correspondientes al electrón; en vez del desplazamiento y usó la función de onda ψ.

Pero
λ = h/p = h/mc,
o sea que:
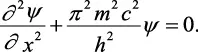
Además, la energía cinética es
(1/2)mv2 = EK ,
así que:

y también la energía cinética EK es igual a la energía total E menos la potencial V:
Ek = E – V,
así que:
 (2.3)
(2.3)
La ecuación 2.3 es la ecuación no relativista de las ondas para el electrón y es la famosa ecuación de Schrödinger independiente del tiempo. La ecuación dependiente del tiempo es la fundamental en mecánica cuántica, pero en este contexto basta con la ecuación 2.3 o su forma tridimensional:
 (2.4)
(2.4)
Antes de dar una interpretación física de la función de onda, se debe recordar el principio de incertidumbre de Heisenberg. Este principio afirma que la precisión con la que pueden realizarse mediciones físicas posee una limitación inherente a la misma, es decir, existe una inevitable falta de certeza en cuanto al resultado de las observaciones. Esto no se refiere al límite de error de las mediciones, que de alguna manera se puede acercar a cero. La incertidumbre a que alude el principio es de una naturaleza mucho más profunda y es inherente a las leyes fundamentales de la naturaleza. Supóngase que se determina la coordenada x de una partícula con una precisión Δx y simultáneamente se mide la componente en x del momento, con precisión Δpx. El principio de incertidumbre establece que en una medición simultánea, los errores mínimos de las mediciones están dados por:
Δpx Δx = h/2π = ħ. (2.5)
El principio no impone ninguna condición a la precisión con que se puede medir la posición Δx (olvidando las consideraciones prácticas). La restricción consiste en que, cuanto más precisamente se trata de determinar la posición, tanto mayor es la incertidumbre que se introduce en el conocimiento simultáneo del momento, y viceversa.
Por supuesto, el principio de incertidumbre impone una duda significativa únicamente en el dominio submicroscópico ħ (llamada hache barra).
Por ejemplo, la incertidumbre en la medida de posición de una masa de 1 kg cuya velocidad tenga una imprecisión de 1 m / s, es de 10–34 m, que es nada. Sin embargo, para un electrón en órbita en un átomo de H, la incertidumbre es del orden de 10–10 m, que es el tamaño del átomo, o sea que la incertidumbre es mayor que la órbita. Los detalles de este principio, empero, están fuera del alcance de esta breve introducción.
Volviendo al tema de la función de onda ψ, debe anotarse que las soluciones de la ecuación de Schrödinger no son reales, sino complejas, o sea que las ondas no son cantidades físicas reales que se pueden medir, sino símbolos matemáticos muy convenientes que permiten calcular el comportamiento de las partículas. La naturaleza compleja de la solución de la ecuación de onda impide identificar la onda misma con una cantidad física real. Una analogía muy conocida sirve para ilustrar este punto. Las ecuaciones que gobiernan el comportamiento de una viga bajo tensiones son de la misma forma que las que controlan las propiedades de las películas elásticas o burbujas. Aunque las propiedades de una viga dada pueden definirse imaginando una burbuja adecuada, nadie va a pensar que los ingenieros construyen puentes con tales burbujas. Del mismo modo, en mecánica ondulatoria se usa el hecho de que las ecuaciones que gobiernan el comportamiento de la onda tienen la misma forma que las que controlan las partículas, pero no implica que estas sean ondas.
La solución de la ecuación de Schrödinger independiente del tiempo, para una función de energía potencial V dada, que describe la situación física, consiste en hallar las soluciones Y(x, t) de la ecuación diferencial 2.4.
Para obtener una solución precisa de un problema físico es necesario obtener no solamente la función matemática ψ(x), sino también instrucciones concisas sobre cómo expresar ψ. O sea que se requiere cierto método para transformar las soluciones, que son cantidades imaginarias, en propiedades observables. Esto se hace con un postulado y no con una identidad que se pueda probar formalmente. Este postulado se debe a Born y dice que la probabilidad de hallar la partícula en el intervalo entre x y (x + dx) es:
P(x, t) = ψ(x, t) ψ*(x, t)dx,
donde ψ(x, t) es la solución de la ecuación de onda de la partícula y ψ* es la conjugada compleja de esta función de onda.
Ahora, la presencia de la partícula en una región es una propiedad mensurable, de modo que la probabilidad P debe ser real, y lo es porque si cualquier complejo q = a + bi, se multiplica por su conjugado q* = a – bi, se obtiene un real:
qq* = (a + bi) (a – bi) = a2 – b2 = /q/2.
Por esta razón, la interpretación que se acepta universalmente es que /ψ/2dx es la probabilidad de observar el electrón en el intervalo comprendido entre x y (x + dx), de manera que /ψ/2 es una densidad de probabilidad.
Читать дальше



 (2.2)
(2.2)
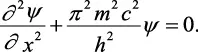

 (2.3)
(2.3) (2.4)
(2.4)