1 ...8 9 10 12 13 14 ...51 La solución general de esta ecuación es:
ψn = An sen Knx, (2.11)
donde An = constantes, Kn = nπ/L y n = 1, 2, 3, 4...
El valor de n no puede ser cero, puesto que significaría la ausencia de partículas en la caja (ψ2 = 0).
Que esta función satisface la ecuación de Schrödinger se puede mostrar reemplazando la ecuación 2.11 en la ecuación diferencial.
Como
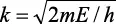 o E = h2k2/2m,
o E = h2k2/2m,
los niveles de energía permitida son:
En = (1/2m) (πh/L)2 n2, (2.12)
con n = 1, 2, 3…
Así, se han determinado la función ψ y el valor de la energía que satisfacen la ecuación diferencial. Las únicas funciones de onda que caben exactamente entre
x = 0 y x = L son los que corresponden a estas energías.
Si L es muy grande, los niveles de energía se acercan entre sí, es decir, las diferencias entre los niveles de energía disminuyen y en el límite L → ∞ la partícula sería libre, porque las energías permitidas no presentarían discontinuidades. Por otro lado, si L es pequeña, las energías y los momentos estarán muy separados.
De la ecuación 2.12 se ve que la función de onda correspondiente a la menor energía, o el estado fundamental, no tiene nodos (n = 1). El estado siguiente (que es el primer estado excitado) tiene uno (n = 2); los segundos estados excitados poseen dos nodos (n = 3), etc. (véase figura 2.10). Cuanto mayor es el número de nodos, tanto más rápido se curva la función de onda y tanto mayor es la curvatura o segunda derivada. Como la segunda derivada de ψ (es decir, ψ″) es proporcional a la energía cinética, resulta que la función de onda que tiene más nodos por unidad de longitud es la que tiene más energía.
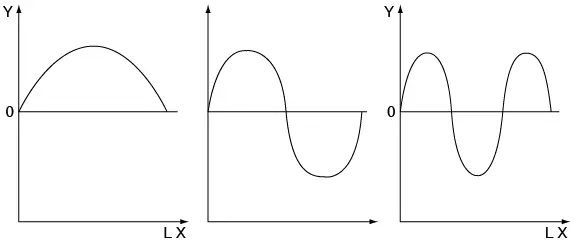
Figura 2.10 Funciones de onda para el estado elemental y para los estados excitados de menor energía, correspondientes a una partícula en una caja
Préstese atención al hecho de que la energía de una partícula que cumple las leyes de la mecánica cuántica solo puede tener un número definido de valores caracterizados por el coeficiente entero n. Esta cuantización de la energía resulta al solucionar la ecuación de Schrödinger, aunque la ecuación misma no contenga coeficientes enteros n.
2.2.3. La partícula en una caja tridimensional
La existencia de niveles discretos de energía para un electrón en un átomo se hace clara con la solución anterior en una caja unidimensional. Pero para explicar otras características de la estructura atómica es aconsejable considerar el movimiento de la partícula en una caja tridimensional.
En este caso, la partícula se confina en un espacio comprendido en una caja potencial, que es un cubo de lado L. El origen de coordenadas es una esquina del cubo. La energía potencial de la partícula dentro del cubo es constante; fuera de él, el potencial es infinitamente grande y, por consiguiente, la partícula no puede estar fuera del cubo en ninguna circunstancia.
Como en el caso anterior, esto es hipotético. Pero existen fenómenos para los cuales estas condiciones se cumplen hasta cierto punto; por ejemplo, el movimiento de los electrones de conducción en un pedazo de metal. Estos electrones se mueven en todas las direcciones, pero no salen de la pieza de metal; por eso, este modelo se usa en la teoría del estado metálico.
La solución tridimensional se logra expresando la función de onda como el producto de tres funciones unidimensionales.
Ψ (x, y, z) = X(x)Y(y)Z(z).
Haciendo las operaciones convenientes se llega a:
X(x) = Ax sen(nxπx/L) para nx = 1, 2, 3,…
Y(y) = Ay sen(nyπy/L) para ny = 1, 2, 3,…
Z(z) = Az sen(nzπz/L) para nz = 1, 2, 3,…, y
E = Ex + Ey + Ez = (nx2 + ny2 + nz2)h2/2L2. (2.13)
Como en el caso de la caja unidimensional, los valores nx, ny y nz solo pueden ser números enteros. De este modo, al pasar del problema unidimensional al tridimensional, aparecen tres características enteras en la expresión de la función de onda. Tal resultado tiene un significado general. El tratamiento cuántico ha demostrado que la función de onda de una partícula siempre contiene parámetros adimensionales que pueden tomar un número de valores enteros. Estos valores son los denominados números cuánticos. La cantidad de números cuánticos contenidos en la solución es igual a la de grados de libertad de la partícula. En el caso unidimensional, solo hay un grado de libertad; en el espacio, el movimiento traslacional tiene tres grados de libertad; si, además, la partícula puede rotar sobre su eje, hay un cuarto grado de libertad.
En el caso unidimensional, los números cuánticos corresponden a energías diferentes; en el tridimensional, hay estados caracterizados por diferentes números cuánticos, excepto uno, y la misma energía. De este modo, para nx = 2, ny = 1 y
nz = 1, la energía de la partícula será la misma que para nx = 1, ny = 2 y nz = 1. Si la energía corresponde a varios estados diferentes (caracterizados por distintas funciones de onda) se dice que el nivel de energía está degenerado. Según el número de estados, la degeneración puede ser doble, triple, etc.
2.2.4. El pozo de potencial
En la sección 2.2.2 se vio que las condiciones de contorno ψ(0) = ψ(L) = 0 llevan a niveles de energía cuantizados. Séase ahora el caso en que las paredes de potencial se encuentran en x = 0 y x = L, pero no son infinitas, sino finitas (véase figura 2.11). Las constantes en la energía se eligen de modo que V = 0 para x < 0 y para x > L.
Para 0 < x < L, el potencial es negativo (es el potencial de un pozo cuadrado), esto es, V = –V0; y supóngase que en este potencial hay una partícula cuya energía total es negativa, 0 > E = –V0 (véase figura 2.11). Para 0 < x < L, la ecuación de Schrödinger es:
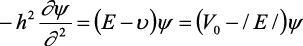
o
ψ′′ +k21ψ = ٠,
con 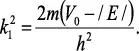
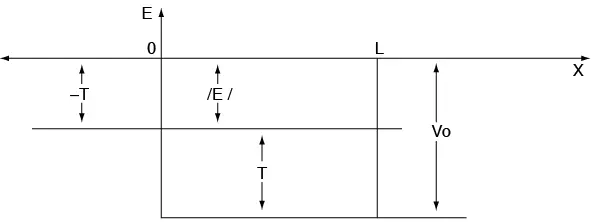
Figura 2.11 Pozo de potencial
La solución general es:
ψ = Acosk1x – Bsenk1 x.
En las regiones x < 0 y x > L, la energía cinética es negativa: T = E – V = –/E/
En mecánica newtoniana, la energía cinética no puede ser nunca negativa: –(1/2) mv2; la partícula no podría existir en la región donde x < 0 o x > L. Sin embargo, en mecánica cuántica, la energía cinética es:
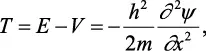 (2.14)
(2.14)
y puede ser negativa si ψ″ tiene el mismo signo que ψ. Así que la probabilidad de observar la partícula en una zona en la cual la energía es negativa, es finita.
O sea que, a diferencia del pozo de potencial infinito, la onda puede atravesar una “barrera” de potencial y salir al otro lado, como se ve en la figura 2.12. Este efecto túnel se ha observado experimentalmente (Binnig y otros, 1982).1
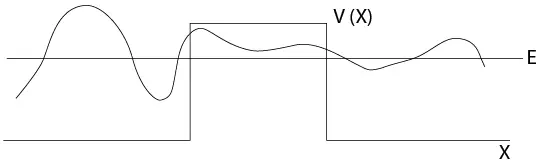
Figura 2.12 Efecto túnel de una onda
Читать дальше

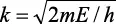 o E = h2k2/2m,
o E = h2k2/2m,
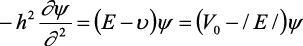
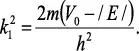

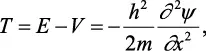 (2.14)
(2.14)