Asdrúbal Valencia Giraldo - Ciencia de los metales

Con estas nociones sobre números cuánticos, se tiene una idea acerca de cómo los electrones se distribuyen en un átomo, con las aplicaciones que esto implica en la formación de los enlaces entre los átomos, la naturaleza de este enlace y las características que ello proporciona a los materiales así formados. Infortunadamente, las razones de espacio impiden proseguir con este interesante tema y a continuación se considera fundamentalmente la naturaleza del comportamiento electrónico de los metales.

2.3. Teoría del electrón libre

Como se anotó al principio, la aplicación de la mecánica cuántica a los problemas del estado sólido trajo inmensos avances en su conocimiento. Así, los principios establecidos en las secciones anteriores tienen como propósito sentar las bases para la descripción del comportamiento del electrón en los metales.

La primera teoría importante sobre los metales fue propuesta por el físico alemán Paul Drude (1863-1906) (véase figura 2.17), en 1900, poco después del descubrimiento del electrón. Según él, los electrones de un metal se movían libremente como si constituyeran un gas. Este concepto fue ampliado por el físico holandés Hendrik Antoon Lorentz (1853-1928) (véase figura 2.17), quien aplicó la teoría cinética clásica de los gases al gas electrónico del metal. La introducción de la mecánica ondulatoria condujo a Sommerfeld, en 1928, a la formulación de la teoría cuántica del electrón libre, teniendo en cuenta que el electrón se comporta como una onda, hecho que ya había sido comprobado experimentalmente (Thomson, 1927).

Figura 2.17 Paul Drude (a la izquierda) propuso la teoría del electrón libre, que fue complementada por Hendrik Antoon Lorentz (a la derecha).

Fuentes: Wikipedia (s. f. 8).

Hacia la misma época, el físico suizo Félix Bloch (1905-1983) (véase figura 2.18) inició la teoría zonal, que fue elaborada por el francés León Brillouin (1889-1969) (véase figura 2.18). Esta teoría considera el movimiento de los electrones en un campo periódico de potencial como el que se presenta en una red cristalina.

En la teoría de Drude y Lorentz, el metal es como una crema con pasas, donde estas son los núcleos (o iones) y aquella sería el gas electrónico. El comportamiento de estos electrones libres es de muchas maneras análogo al de las moléculas gaseosas; el potencial electrónico en el interior del metal se supone uniforme, y en este campo uniforme los electrones se mueven según las leyes de la teoría cinética de los gases (estadística de Maxwell-Boltzmann).

Figura 2.18 Félix Bloch y León Brillouin. Estos físicos desarrollaron la teoría electrónica de zonas.

Fuentes: Wikipedia (s. f.3).

Pero hay una diferencia significativa: aquí las colisiones entre los electrones se desprecian y solo importan las que se dan entre los electrones y los iones.

Normalmente, los electrones se mueven al azar en el campo uniforme; sin embargo, cuando se aplica un voltaje al metal, son atraídos hacia el lado positivo, originando una corriente eléctrica. Los impactos con los átomos evitan una aceleración indefinida y con un gradiente de tensión dado logran una velocidad fija, que es una corriente estacionaria proporcional al voltaje, como lo establece la ley de Ohm.

Debe notarse que las atracciones coulómbicas entre los electrones y los iones fijos se desprecian, es decir, el campo periódico se suaviza y la carga positiva se supone distribuida uniformemente en el metal y no localizada en los iones. Por eso, el campo es uniforme, como en el caso de un pozo de potencial. En realidad, este potencial atractivo es de una magnitud relativamente considerable. También se supone que la trayectoria libre media del electrón entre colisión y colisión está gobernada por el espaciamiento reticular del cristal y es independiente de la velocidad del electrón.

Además, se hace una marcada diferencia entre los electrones internos difíciles de arrancar y los exteriores o de valencia; solo estos son libres en este modelo, los otros no cambian respecto al estado atómico.

No obstante las simplificaciones anotadas, la teoría fue útil en la predicción de propiedades como las conductividades eléctrica y térmica, las propiedades ópticas y la capacidad calórica, como se verá a continuación con la teoría ya más elaborada.

En el modelo de Sommerfeld se supone que los electrones se mueven en un espacio libre de campo dentro del material; en otras palabras, también se desprecian las interacciones coulómbicas entre los electrones y los iones de la red. Pero en este modelo, los electrones experimentan fuerzas que tienden a evitar que escapen del metal y este comportamiento está representado por una barrera de potencial en la superficie. Además, los electrones obedecen a las leyes de la mecánica ondulatoria. El modelo más simple para este caso es el del pozo de potencial unidimensional, donde el electrón está contenido en una caja x = 0 a x = L, con barreras de potencial infinito (véase figura 2.19).

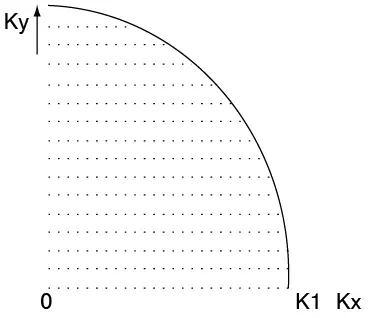
Figura 2.19 Los valores permitidos del vector de onda K ocupados por los electrones

Los resultados de la caja tridimensional (ecuación 2.13) se pueden usar para determinar el número de electrones que se puede acomodar en una caja en un intervalo particular de valores de energía. La ecuación 2.13:

E = (nx2 + ny 2+ nz2) h2/2L2,

se puede escribir como:

E = (Kx2+ Ky2 + Kz2)ħ2 /2m, (2.16)

donde

K x = 2πnx /Lx

Ky = 2 πny/Ly

K z = 2πnz /Lz

ħ = h/2π.

Es necesario ver el significado de los tres números de onda que especifican un estado particular. En una dimensión, K y el momento p están relacionados por:

p = kK = h/λ;

en tres dimensiones, p y K son vectores:

p = hk y

k = Kx + Ky + Kz,

k2 = Kx2+ Ky2 + K z2. (2.17)

Reemplazando (2.17) en (2.16),

E = k2 ħ2/2m. (2.18)

Los vectores como K se pueden representar en un diagrama tridimensional, donde se grafican los valores de Kx, Ky y Kz. Las varias combinaciones de Kx + Ky + Kz

producen un arreglo de puntos en este vector o espacio K, como se muestra en la figura 2.19. Cada vector está representado por la línea trazada desde el origen hasta un punto y cada una representa un solo estado cuántico y una solución de la ecuación de onda. Se sabe que cada estado cuántico únicamente puede contener dos electrones de espín diferente o sea que la figura 2.10 representa todos los estados cuánticos en un solo diagrama.

La representación de la solución en el espacio K incluye tanto la descripción ondulatoria como la corpuscular (partícula). Como cada vector K es paralelo a un momento p y su magnitud es Kp, la única diferencia entre un espacio de momentos y un espacio K es un factor K.

La relación 2.18 entre K y la energía permite el uso del espacio K para representar también los estados energéticos. Como la ecuación 2.18 solo incluye la magnitud de K, todos los vectores que tengan la misma magnitud tienen la misma energía.