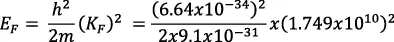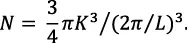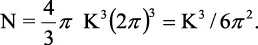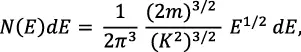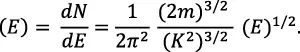Todos los estados residen en una esfera cuyo radio es K. Dado que los electrones obedecen el principio de exclusión, en un estado sólo puede haber dos electrones de espín contrario y a 0 °K3 los electrones ocupan los estados de energía más bajos.
Por esta razón, los estados de menor energía con menor K se llenan primero, y así sucesivamente, hasta el máximo K ocupado, con la energía más elevada. Para valores grandes de K hay muchos estados con el mismo K (o sea el mismo valor de energía) y todos están sobre la superficie de una esfera. Dentro de la esfera, todos los estados están ocupados; fuera de ella, todos están vacíos (véase figura 2.20). La superficie de la esfera se llama superficie de Fermi. El vector de onda de Fermi (KF) es el radio y la energía de los estados que están en la superficie de Fermi es la energía de Fermi (EF).
Todos los electrones en una pieza de metal yacen en estados dentro de la esfera de Fermi, con radio KF y un volumen
VF = (4/3)πKF3. (2.19)
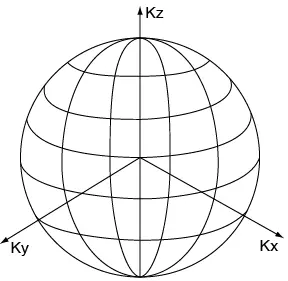
Figura 2.20 La esfera de Fermi. La define el número de onda.
Este volumen contiene estados espaciados 2π/L en una dimensión; por consiguiente, el volumen por estado es (2π/L). Cada estado puede contener dos electrones y, así, el volumen en el espacio K para todos los N electrones de la pieza es:
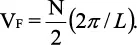 (2.20)
(2.20)
Igualando 2.19 y 2.20:
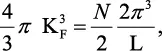
KF = (3π2N/L3)1/3 en donde N/L3 es la densidad de cargas libres n (densidad de electrones de valencia) que se calcula con la ecuación 2.21.
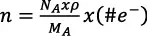 (2.21)
(2.21)
En donde NA es el número de Avogadro (6.02x1023), ρ es la densidad del elemento, MA es la masa atómica del elemento y #e- es la cantidad de electrones de valencia por átomo o electrones en el último nivel de energía.
La energía de Fermi es:
EF = h2kF2/2m = h2(3π2n3)2/3/2m
En donde h es la constant de Plank (6.64x10-34 J/s) y m es la masa del electrón (9.1x10-31 kg).
Por ejemplo, para el Aluminio (Al) con número atómico Z=13, densidad
ρ = 2.7gr/cm3 y masa atómica MA=27gr/mol:
La distribución electrónica es 1S2 2S2 2P6  , por lo tanto tiene 3 electrones de valencia por átomo y la densidad de cargas libres es:
, por lo tanto tiene 3 electrones de valencia por átomo y la densidad de cargas libres es:
n = [(3 electrones de valencia/átomo) × (6,02 × 1023 átomo/mol) x
(2.7gr/cm3)]/ 27 gr/mol = 1,8068 × 1023 electrones / cm3
o en unidades del sistema internacional 1,8068 × ١٠29 electrones / m3
KF = [3π2 × 1,8068 × 1029]1/3 = 1,749 × 1010 m–1,
y la energía de Fermi es:
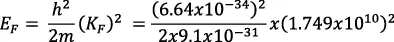
EF =1,867 × 10-18 Joules o 11.7 electronvoltios
2.3.1. Densidad de los estados
En la sección precedente se mostró que el tamaño de la esfera de Fermi es grande comparado con el espaciamiento entre puntos en el espacio K. Esto se debe al enorme número de electrones que hay en una pieza de metal, los cuales requieren gran cantidad de estados para acomodarse.
La esfera de Fermi y sus implicaciones se discuten más adelante; por ahora, es necesario considerar que cerca de la superficie de Fermi hay un gran número de puntos sobre la misma superficie esférica y con la misma energía. Esta cantidad es la densidad de estados. Ella se aplica a la unidad de volumen de un metal y mide el número de estados en el intervalo de energía dE. Se denota con N(E)dE y se puede calcular con las ecuaciones ya desarrolladas.
El número de estados dentro de la esfera de radio K, donde cada estado tiene un volumen (2π/L) 3, es:
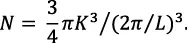
Para el volumen unitario, L3 = 1,
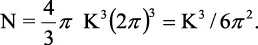
De la ecuación 2.17,
K = (2mE)1/2/K,
y así:
N = (2mE)3/2/(62 K3).
Esto da el número de estados con energía menor que E.
La densidad de estados es el número de estados en el intervalo de energía dE, o sea:
N(E)dE = dN = [(2m)3/2 E1/2 /4π2 K3]dE;
así,
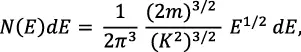
y
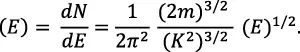
Esta función se gráfica en la figura 2.21 y es una parábola sobre el eje de energía.
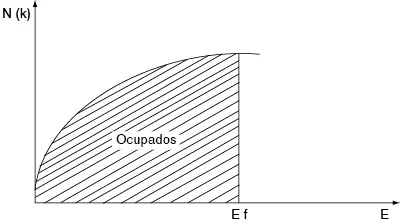
Figura 2.21 Densidad de los estados, con los estados ocupados a temperatura 0 K.
La forma de la curva indica el aumento de la degeneración de los niveles energéticos a medida que la energía se incrementa.
Nótese que la energía es función solamente de la magnitud del vector de onda. El espacio K se usa cuando se desean discutir las propiedades direccionales. Sin embargo, la curva de la figura 2.21 es una buena manera de representar el número de estados ocupados por los electrones en el cero absoluto. En suma, la figura 2.21 muestra la naturaleza de la distribución de los de Sommerfeld. Como se observará, esto cambia al aumentar la temperatura, pero es una base indispensable para comprender las densidades de estado en los átomos polielectrónicos que se combinan para formar el sólido, sea este metálico o no.
2.3.2. Efecto de la temperatura sobre la densidad de los estados
La discusión del modelo del electrón libre se hizo suponiendo que el gas electrónico estaba a una temperatura de cero absoluto (ideal).
Dado que la temperatura es la variable metalúrgica más importante, es necesario determinar el efecto de un aumento de ella sobre el modelo. Esto naturalmente conduce a una relación entre la mecánica ondulatoria y la termodinámica.
Ante todo, debe anotarse que el comportamiento de los electrones se trata con los principios de Maxwell-Boltzmann, es decir, que en el modelo del electrón libre, estos se comportan como partículas distinguibles. Si los electrones se asumen verdaderamente independientes (indistinguibles), la función de distribución adecuada es diferente. Es la distribución Fermi-Dirac, que lleva implícito el principio de exclusión de Pauli.
Al elevar la temperatura, los átomos vibran con amplitudes mayores y la energía asociada es intercambiada entre los átomos y los electrones libres, transformando el contenido energético de estos últimos y excitándolos térmicamente.
Las propiedades térmicas de los metales dependen del número de electrones térmicamente excitados a niveles de energía superiores y ese número se puede calcular con la distribución de Fermi-Dirac.
Читать дальше


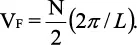 (2.20)
(2.20)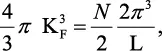
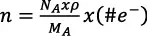 (2.21)
(2.21) , por lo tanto tiene 3 electrones de valencia por átomo y la densidad de cargas libres es:
, por lo tanto tiene 3 electrones de valencia por átomo y la densidad de cargas libres es: