Asdrúbal Valencia Giraldo - Ciencia de los metales

k = nπ/a, (3.6)

donde n = ±1, ±2, ±3,...

Esto se puede ver en la figura 3.4.

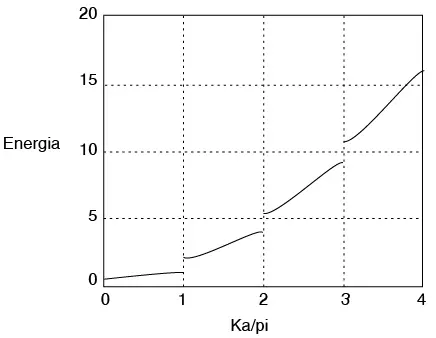
Figura 3.4 Discontinuidades de la parábola del electrón libre

Estas discontinuidades se dan cuando k = nπ/a, donde n = ±1, ±2, ±3,...

Sin embargo, K = 2π/λ; o sea,

nλ = 2a. (3.7)

Esta ecuación es equivalente a la conocida ley de Bragg para difracción, con un ángulo de Bragg de θ = 90°. En otras palabras, si a es el espaciamiento entre planos que son perpendiculares a la dirección de propagación del electrón, entonces 3.7 define la longitud de onda (o la energía) para la cual se da una reflexión total. La ecuación 3.7 podría escribirse teniendo en cuenta que k = 2π/λ; y para cualquier ángulo θ, la relación anterior puede generalizarse:

ksenθ = nπ/α,

donde θ es el ángulo de Bragg.

3.2.3. Zonas de Brillouin

El paralelismo entre la ecuación 3.7 y la ley de Bragg es consecuencia directa de la naturaleza ondulatoria de los electrones. Para entender mejor esta relación, es bueno reescribir la ecuación 3.7 para n = 1, usando la notación cristalográfica. La dirección cristalográfica del movimiento de los electrones se denota con el subíndice [uvw], así que:

k[uvw] = π/d[hkl], (3.8)

donde d[hkl] es el espaciado interplanar de los planos que son normales a uvw, en dos direcciones. Las direcciones se denotan [uv] y los “planos” se conviertan en líneas (hk).

Considérese el “cristal” bidimensional, con una red cuadrada, mostrado en la figura 3.5a. Así mismo, electrones que se mueven en la dirección [21], que es normal a las líneas de puntos (21).

a 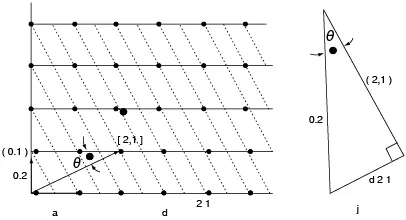b

Figura 3.5 Representación de un “cristal” bidimensional

De acuerdo con la relación 3.8, la reflexión total de los electrones se da cuando el número de onda satisface la condición

K[21] = π/d(21). (3.9)

De modo alterno, séanse las líneas sólidas (01) que forman el ángulo θ con [21]. Una vista aumentada del triángulo que relaciona al espaciado interlineal de (01), con d(21), que se mide en una dirección paralela a [211], se muestra en la figura 3.5b.

Es claro que

d(21) = asenθ.

Sustituyendo este valor en la ecuación 3.9:

K[21] = 2π/λ = π/asenθ,

que es la ley de Bragg para la reflexión desde líneas que tengan un espaciado interlineal de a.

De lo anterior se tiene que la condición 3.6, que determina las discontinuidades en los intervalos de energía permitida de los electrones en un cristal, puede ser interpretada para indicar o bien la reflexión total de los electrones por los planos que son normales a la dirección de propagación, o bien las reflexiones de Bragg por otros planos cristalográficos. Obviamente, los planos escogidos para esta última interpretación son los planos que reflejan con más fuerza a los electrones.

Para una estructura cristalina constituida por un átomo colocado en los puntos reticulares de una red cúbica primitiva, estos planos son las caras del cubo que pertenecen a la forma {100}. En un cristal cúbico de cara centrada sencilla seran los planos en {111} y {200}, y en un cristal de cuerpo centrado serán los planos {110}. Los poliedros formados por estos planos son llamados primeras zonas de Brillouin de estos cristales. Las figuras 3.6a y 3.6b muestran las primeras zonas de Brillouin de un metal fcc y bcc respectivamente.

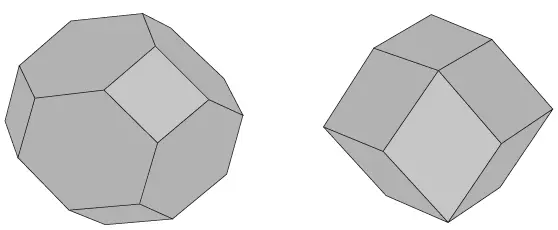
Figura 3.6 Primeras zonas de Brillouin en un metal a. fcc y b. bcc.

Debe anotarse que otros planos en el cristal también pueden reflectar los electrones. En efecto, para energías mayores y, en consecuencia, números de onda más altos, se ve claramente en la ecuación 3.9 que se requieren valores menores de d para mantener la igualdad.

Así que otro conjunto de planos, menos separados, es necesario para reflejar los electrones que tienen energías pertenecientes a la segunda zona permitida, y de igual manera con los demás. Los poliedros formados por estos planos son llamados la segunda, la tercera, etc., zonas de Brillouin del cristal. En honor de León Brillouin, su creador (véase figura 3.7), se usan estos poliedros para la discusión de las energías en los cristales (véase figura 3.8).

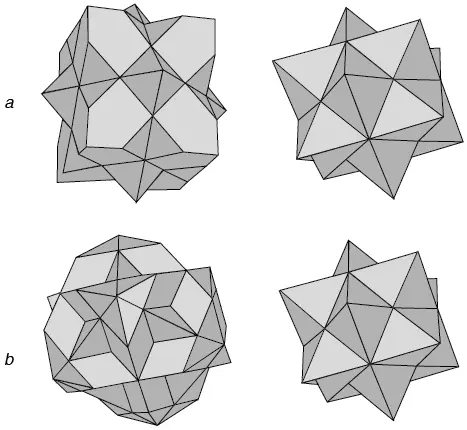
Figura 3.7 a. Segundas zonas de Brillouin en cristales fcc y bcc; b. Terceras zonas de Brillouin en cristales fcc y bcc.

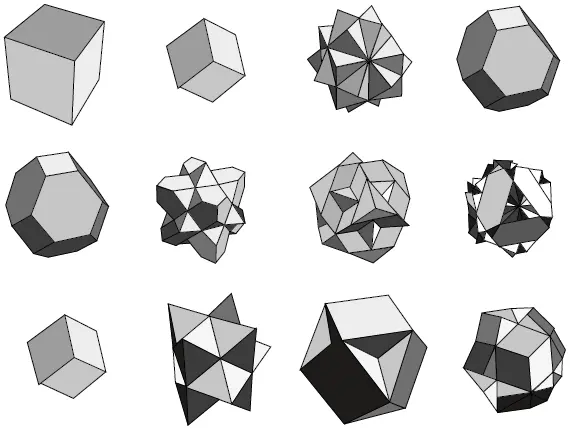
Figura 3.8 Zonas de Brillouin

3.2.2.1. El espacio K

El espacio K, del que ya se habló en la sección 2.5, es especialmente adecuado para la representación de las zonas de Brillouin. En el caso de los cristales cúbicos, es convención seleccionar los tres ejes x, y y z, paralelos a los tres ejes cristalográficos equivalentes a a, y denotar las direcciones paralelas a estos ejes con los subíndices

x, y, z. De acuerdo con eso, la condición 3.6 para estas tres direcciones es:

kx = ky = kz = ± π/a, (3.10)

donde el signo ± corresponde a valores positivos o negativos de x, y y z.

Conviene más usar los números de onda kx, ky y kz como ejes de coordenadas para la construcción, como se hizo en las figuras 3.5 y 3.6, de las zonas de Brillouin. El espacio determinado por estos ejes, como se anotó, se llama espacio K, y como las distancias en este espacio son el recíproco de las distancias en el cristal, de acuerdo con la ecuación 3.9, también es llamado espacio o red recíproca. Nótese que para un electrón libre esto es proporcional al espacio de momento discutido antes.

El espacio k, definido por kx, ky se muestra en la figura 3.8. La primera zona de Brillouin para un cristal cúbico simple es un cubo que se presenta en la sección transversal de esta figura. La segunda zona de Brillouin para un cristal simple es un dodecaedro limitado por {110}; su sección transversal se ve en el plano xy en la figura 3.8. Nótese que la segunda zona queda fuera de la primera zona en el espacio k, porque está limitada por los planos {110}, que tienen una distancia interplanar menor que los planos {100}. Esto, por supuesto, es debido a las relaciones recíprocas entre las distancias en el cristal y las que se presentan en el espacio k.

3.2.2.2. Superficies de Fermi

Como se anotó en la sección 3.2.2, una propiedad muy útil del espacio K es que la relación entre número de onda y energía puede usarse para mostrar la distribución de los valores de energía permitida para los electrones de valencia. Esto se debe a que la energía está relacionada con k, como lo muestra también la figura 3.9.

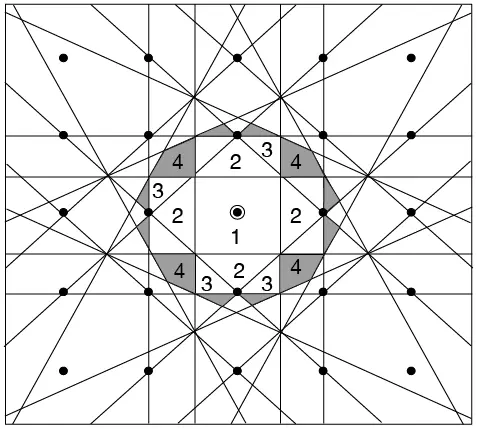
Figura 3.9 Las tres primeras zonas de Brillouin en una red cuadrada bidimensional