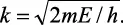1 ...7 8 9 11 12 13 ...51 Como toda función de probabilidad debe estar normalizada,
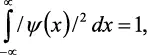 (2.6)
(2.6)
ya que la probabilidad de encontrar la partícula en algún punto del eje x debe ser igual a la unidad.
La normalización de la solución de la ecuación de Schrödinger se hace multiplicando por un factor apropiado, que es una constante y que se determina usando la ecuación 2.6. Pero si /ψ/2 es una probabilidad, ¿cuál es el significado de la función ψ misma? La respuesta es que ψ no tiene interpretación directa, es decir, no tiene significado físico, aunque /ψ/2 sí lo tiene.
En resumen, la función de onda ψ es finita, continua invariable y se hace cero cuando la partícula no se puede hallar. Por ejemplo, si se considera el movimiento de un electrón de un átomo, ψ se hace cero a una distancia infinitamente lejana del núcleo. Además, es una onda cuyo cuadrado describe la probabilidad de los diversos resultados posibles de una observación, pero no dice nada sobre la trayectoria de la partícula, sus coordenadas o su velocidad en un momento dado; tales conceptos no tienen significado en mecánica cuántica. Sin embargo, los conceptos de masa, energía y momento angular de la partícula conservan su importancia.
2.2. Soluciones de la ecuación de Schrödinger
La función de onda ψ es tridimensional. Además, las soluciones de esta ecuación para los problemas de teoría atómica y estructura molecular son muy complicadas, y no se intentarán de ninguna manera en este texto; sin embargo, para estudiar el átomo y, por tanto, la materia, es necesario analizar la solución de la ecuación de Schrödinger para algunos campos simples.
Se ha discutido el significado de ψ. Ahora póngase atención a los factores que en la ecuación de Schrödinger multiplican o que “operan sobre” ψ, de manera que se ve que ψ no solo contiene información probabilística, sino también sobre las propiedades físicas. Si la ecuación 2.5 se escribe en la forma:
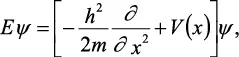
y se compara con la ecuación clásica:
E = EK + V,
resulta que el operador diferencial
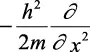
se debe identificar de algún modo con la energía cinética EK.
Por otro lado, la energía potencial es un operador multiplicativo, es decir, una función que multiplica a ψ para transformarla en una nueva función V(x) ψ(x). Entonces, para el movimiento en una dimensión, hay un operador T, relacionado con la energía cinética, que es:
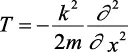 . (2.7)
. (2.7)
El operador de la energía total se llama operador de Hamilton (H), y se define por:
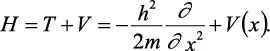
Así, la solución de la ecuación de Schrödinger,
Hψ = Eψ,
es el problema de encontrar los valores propios del operador H. Esto se hará para algunos casos sencillos en las secciones que siguen.
2.2.1. La partícula libre
La función de onda más simple es la correspondiente a una partícula libre, es decir, una partícula que se mueve en ausencia de todo potencial. Con V = 0, la ecuación de Schrödinger se reduce a:
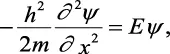
o también a:
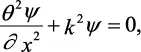 (2.8)
(2.8)
donde
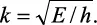
La ecuación 2.8 es la ecuación de Helmholtz para el oscilador armónico y es exactamente igual a la ecuación 2.2 del desplazamiento de una cuerda estirada. La solución general es:
ψ = Acoskx + Bsenkx,
donde A y B pueden ser números complejos.
Si se hace B = Ai, se obtiene una solución especial:
ψ = Acoskx + Aisenkx = A ikx.
Como o  es la magnitud de p, el momento de una partícula libre se puede escribir
es la magnitud de p, el momento de una partícula libre se puede escribir
ψ = Aipx/h
o
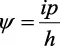
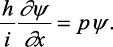 (2.9)
(2.9)
Así, en la componente x, el operador momento es:
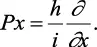 (2.10)
(2.10)
De las ecuaciones 2.7 y 2.10 se ve que
T = p2/2m.
Además, si se busca a /ψ/2 para la ecuación 2.9,
/ψ/2 = /AE ipx/h/2 = /A/2,
que no solo es real, sino también independiente de x. Por tanto, todas las posiciones x son probables.
Como se conoce el incremento p (o sea Δp = 0), según el principio de incertidumbre, Δx = ∞, que es lo establecido. Así, para una partícula libre no es necesario poner restricciones en su función de onda respecto a E o a p, pues no hay condiciones de borde; todo x es posible. En otras palabras, los niveles de energía de una partícula libre no están cuantizados; de esta manera, dicha partícula es similar a las ondas que se desplazan en una cuerda.
2.2.2. La partícula en una caja unidimensional
En este modelo, la partícula (por ejemplo, un electrón) solo se puede mover en una dirección, es decir, a lo largo de un eje, que puede ser el x, desde x = 0 hasta x = L. Dentro de los límites de esta región, la energía potencial de la partícula es uniforme, por lo que es conveniente tomarla igual a cero. Fuera de esta región, el potencial V que actúa sobre la partícula es infinitamente elevado; esto significa que ella no puede ir más allá de la región 0 < x < L (ello requeriría un aumento infinito en la energía).
Matemáticamente, esto se representa como (véase figura 2.9):
V(x) = 0 para 0 ≤ x ≤ 0
V(x) = ∞ para x > L o x < 0.

Figura 2.9 Pozo potencia, unidimensional
La partícula está confinada en la región entre 0 y L, pero se comporta como una partícula libre. Con V(x) = ∞, la única solución de la ecuación de Schrödinger es ψ = 0.
Como ψ debe ser continua, en la región 0 ≤ x ≤ L la función de onda debe satisfacer las condiciones del contorno:
ψ (0) = ψ (L) = 0.
Como en 0 < x < L se da que V = 0, la ecuación es la misma que la de la partícula libre:
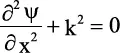 ,
,
con 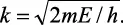
Читать дальше

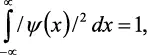 (2.6)
(2.6)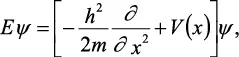
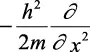
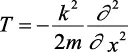 . (2.7)
. (2.7)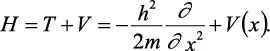
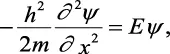
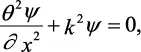 (2.8)
(2.8)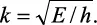
 es la magnitud de p, el momento de una partícula libre se puede escribir
es la magnitud de p, el momento de una partícula libre se puede escribir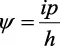
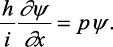 (2.9)
(2.9)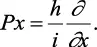 (2.10)
(2.10)
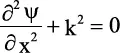 ,
,