Max Diem - Quantum Mechanical Foundations of Molecular Spectroscopy

The incorporation of this uncertainty into the picture of the motion of microscopic particles leads to discrepancies between classical and quantum mechanics: classical physics has a deterministic outcome, which implies that if the position and velocity (trajectory) of a moving body are established, it is possible to predict with certainty where it is going to be found in the future. This principle certainly holds at the macroscopic scale: if the position and trajectory of a macroscopic body, for example, the moon, are known, it is certainly possible to calculate its position six days from now and to send a spaceship to this predicted position.

Quantum mechanical systems, on the other hand, obey a probabilistic behavior. Since the position and momentum can never be determined simultaneously at any point in time, the position (or momentum) in the future cannot be precisely predicted, only the probability of either of them. This is manifested in the postulate that all properties, present or future, of a particle are contained in a quantity known as the wavefunction Ψ of a system. This function, in general, depends on spatial coordinates and time; thus, for a one‐dimensional motion (to be discussed first), the wavefunction is written as Ψ( x , t ). The probability of finding a quantum mechanical system at any time is given by the integral of the square of this wavefunction: ∫Ψ( x , t ) 2d x . This is, in fact, one of the “postulates” on which quantum mechanics is based to be discussed next. Different authors list these postulates in different orders and include different postulates necessary for the description of quantum mechanical systems [1]. Quantum mechanics is unusual in that it is based on postulates, whereas science, in general, is axiom‐based.

Postulate 1: The state of a quantum mechanical system is completely defined by a wavefunction Ψ( x, t ). The square of this function, or in the case of complex wavefunction, the product Ψ*( x, t ) Ψ( x, t ), integrated over a volume element d τ (= d x d y d z in Cartesian coordinates or sin 2 θ d θ d φ in spherical polar coordinates) gives the probability of finding a system in the volume element d τ . Here, Ψ*( x, t ) is the complex conjugate of the function Ψ( x, t ). This postulate contains the transition from a deterministic to probabilistic description of a quantum mechanical system. The wavefunctions must be mathematically well behaved, that is, they must be single‐valued, continuous, having a continuous first derivative, and integratable (so they can be normalized).

Postulate 2: The classical linear momentum expression, p = m v, is substituted in quantum mechanics by the differential operator , defined by

(2.2)

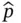operating (or being applied to) the wavefunction Ψ( x, t ). In Eq. (2.2), i is the imaginary unit, defined by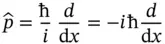 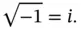Equation (2.2)often is considered the central postulate of QM.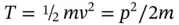

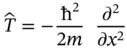
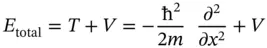
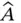The form of Eq. (2.2)can be made plausible from equations of classical wave mechanics, de Broglie's equation ( Eq. [1.10]) and Planck's equation ( Eq. [1.7]), but cannot be derived axiomatically. It was the genius of E. Schrödinger to realize that the substitution described in Eq. (2.2)yields differential equations that had long been known and had solutions that agreed with experiments. In the Schrödinger equations to be discussed explicitly in the next chapters (for the H atom, the vibrations and rotations of molecules, and molecular electronic energies), the classical kinetic energy T given by

(2.3)

is, therefore, substituted by

(2.4)

which is, of course, obtained by inserting Eq. (2.2)into Eq. (2.3). The total energy of a system is given as the sum of the potential energy V and the kinetic energy T :

(2.5)

Postulate 3: All experimental results are referred to as observables that must be real (not imaginary or complex). An observable is associated with (or is the “eigenvalue” of) a quantum mechanical operator . This can be written as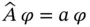

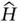(2.6)

where a are the eigenvalues and ϕ the corresponding eigenfunctions. The terms “operator,” “eigenvalues,” and “eigenfunctions” are terminology from linear algebra and will be further explained in Section 2.3where the first real eigenvalue problem, the particle in a box, will be discussed. Notice that the eigenfunctions often are polynomials, and each of these eigenfunctions has its corresponding eigenvalue.

In this book, following generally accepted notations, the total energy operator is generally identified by the symbol and referred to as the Hamilton operator, or the Hamiltonian, of the system. With the definition of the Hamiltonian above, it is customary to write the total energy equation of the system as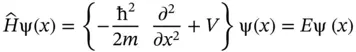

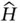(2.7)

Equation (2.7)implies that the energy “eigenvalues” E are obtained by applying the operator on a set of (still unknown) eigenfunctions ψ that are here assumed to be time‐independent and a function of spatial coordinates x only, ψ( x ). Solving the differential equations given by Eq. (2.7)yields the eigenfunctions ψ iand their associated energy eigenvalues E i.

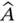Postulate 4: The expectation value of an observable a , associated with an operator , for repeated measurements, is given by

(2.8)