1 ...6 7 8 10 11 12 ...17 b) The resonance frequency in NMR and EPR depends on the magnetic field strength.
In this table, NMR and EPR stand for nuclear magnetic and electron paramagnetic resonance spectroscopy, respectively. In both these spectroscopic techniques, the transition energy of a proton or electron spin depends on the applied magnetic field strength. All techniques listed in this table can be described by absorption processes although other descriptions, such as bulk magnetization in NMR, are possible as well. As seen in Table 1.1, the photon energies are between 10 −16and 10 −25J/photon or about 10 −4–10 5kJ/(mol photons). Considering that a bond energy of a typical chemical (single) bond is about 250–400 kJ/mol, it shows that ultraviolet photons have sufficient energy to break chemical bonds or ionize molecules. In this book, mostly low energy photon interactions will be discussed, causing transitions in spin states, rotational, vibrational, and electronic (vibronic) energy levels.
Most of the spectroscopic processes discussed are absorption or emission processes as defined by Eq. (1.18):
(1.18) 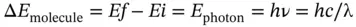
However, interactions between light and matter occur even when the light's wavelength is different from the specific wavelength at which a transition occurs. Thus, a classification of spectroscopy, which is more general than that given by the wavelength range alone, would be a resonance/off‐resonance distinction. Many of the effects described and discussed in this book are observed as resonance interactions where the incident light, indeed, possesses the exact energy of the molecular transition in question. IR and UV/vis absorption spectroscopy, microwave spectroscopy, and NMR are examples of such resonance interactions.
The off‐resonance interactions between electromagnetic radiation and matter give rise to well‐known phenomena such as the refractive index of dielectric materials. These interactions arise since force is exerted by the electromagnetic radiation on the charged particles of matter even at off‐resonance frequencies. This force causes an increase in the amplitude of the motion of these particles. When the frequency of light reaches the transition energy between two states, an effect known as anomalous dispersion of the refractive index takes place. This anomalous dispersion of the refractive index always accompanies an absorption process. This phenomenon makes it possible to observe the interaction of light either in an absorption or as a dispersion measurement, since the two effects are related to each other by a mathematical relation known as the Kramers–Kronig relation. This aspect will be discussed in more detail in Chapter 5.
The normal (nonresonant) Raman effect is a phenomenon that also is best described in terms of off‐resonance models, since Raman scattering can be excited by wavelengths that are not being absorbed by molecules. A discussion of nonresonant effects ties together many well‐known aspects of classical optics and spectroscopy.
The observation of the photoelectric effect and the absorption/emission spectra of the hydrogen atom and the modifications required to formulate the blackbody emission theory were the triggers that forced the development of quantum mechanics. As pointed out in the introduction, the development of quantum mechanics is based on postulates, rather than axioms. The form of some of these postulates can be visualized from other principles, but their adoption as “the truth” came from the fact that they produced the correct results.
1 1 Halliday, D. and Resnick, R. (1960). Physics. New York: Wiley.
2 2 Engel, T. and Reid, P. (2010). Physical Chemistry, 2e. Upper Saddle River, NJ: Pearson Prentice Hall.
3 3 Davisson, C.J. and Germer, L.H. (1928). Reflection of electrons by a crystal of nickel. Proceedings of the National Academy of Sciences of the United States of America 14 (4): 317–322.
1 What is the maximum wavelength of electromagnetic radiation that can ionize an H atom in the n = 2 state?
2 Why is it that any photon with a wavelength below the limiting value obtained in (1) can ionize the H atom, whereas in standard spectroscopy, only a photon with the correct energy can cause a transition?
3 Assume that you carry out the experiment in (1) with light with a wavelength of 10 nm less than calculated in (1). What is the kinetic energy of the photoelectron created?
4 What is the velocity of the electron in Problem 3?
5 Using the de Broglie relation for matter waves, calculate the velocity to which an electron needs to be accelerated such that its wavelength is 10 nm.
6 What percentage of the velocity of light is the velocity in (5)?
7 What is the relativistic mass of this electron?
8 At what velocity is the wavelength of an electron 30 nm?
9 What is the momentum of such the electron in (8)?
10 What is the mass of a photon with a wavelength of 30 nm?
11 What is the momentum of the photon in (10)?
12 Compare and comment on the masses and momenta of the moving particles in Problems (8)–(11).
13 “Frequency doubling” or “second harmonic generation (SHG)” is a little optical trick ( Appendix 3) in which two photons of the same wavelength are squashed into a new photon, while the energy is conserved. Calculate the wavelength of the photon created from frequency doubling of two photons with λ = 1064 nm.
14 “Sum frequency generation (SFG)” is another optical trick ( Appendix 3) in which two photons of different wavelengths are squashed into a new photon while the energy is conserved. Calculate the wavelength of SFG photon created from combining two photons with λ1 = 1064 nm and λ2 = 783 nm.
15 The value of the Rydberg constant, Ry, can be calculated according to where e' = e/√4πεo and where mR is the reduced mass of electron and proton. Perform an analysis of the units of Ry.
16 Which two experiments demonstrate that light has wave and particle character?
17 Which two experiments demonstrate that moving electrons have wave and particle character?
2 Principles of Quantum Mechanics
Quantum mechanics presents an approach to describe the behavior of microscopic systems. Whereas in classical mechanics the position and momentum of a moving particle can be established simultaneously, Heisenberg's uncertainty principle prohibits the simultaneous determination of those two quantities. This is manifested by Eq. (2.1):
(2.1) 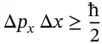
which implies that the uncertainty in the momentum and position always exceeds ħ/2, where ħ is Planck's constant divided by 2 π . Mathematically, Eq. (2.1)follows from the fact that the operators responsible for defining position and momentum, 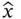 and
and 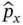 , do not commutate; that is,
, do not commutate; that is, 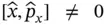 . (This aspect will be discussed in more detail at the end of Section 2.1.) As we shall see later ( Chapter 5), the uncertainty principle also can be rewritten in terms of the uncertainty in energy and lifetime of a spectroscopic state or in frequency and time of a wave.
. (This aspect will be discussed in more detail at the end of Section 2.1.) As we shall see later ( Chapter 5), the uncertainty principle also can be rewritten in terms of the uncertainty in energy and lifetime of a spectroscopic state or in frequency and time of a wave.
Читать дальше

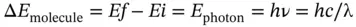
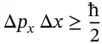
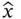 and
and 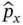 , do not commutate; that is,
, do not commutate; that is, 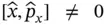 . (This aspect will be discussed in more detail at the end of Section 2.1.) As we shall see later ( Chapter 5), the uncertainty principle also can be rewritten in terms of the uncertainty in energy and lifetime of a spectroscopic state or in frequency and time of a wave.
. (This aspect will be discussed in more detail at the end of Section 2.1.) As we shall see later ( Chapter 5), the uncertainty principle also can be rewritten in terms of the uncertainty in energy and lifetime of a spectroscopic state or in frequency and time of a wave.










