(1.44) 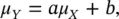
and variance 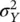 :
:
(1.45) 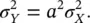
If X is distributed according to a uniform distribution on the interval [ c , d ], X ∼ U ([ c , d ]), and we apply a linear transformation Y = g ( X ) = aX + b , then Y is still distributed according to a uniform distribution Y ∼ U ([ ac + b , ad + b ]), on the interval [ ac + b , ad + b ].
These results are intuitive because if we apply a linear transformation to a distribution, we shift the mean and change the variance, but we do not distort the shape of the distribution. For example, if we assume that porosity is distributed according to a Gaussian distribution (neglecting low probability values for porosity values outside the physical bounds), and we apply a linear rock physics model ( Chapter 2) to compute the corresponding P‐wave velocity distribution, then the distribution of P‐wave velocity is still Gaussian and we can compute the mean and the variance using Eqs. (1.44)and (1.45).
If the transformation is not linear, an analytical solution is not always available. A numerical method to obtain an approximation of the probability distribution of the random variable of interest is the Monte Carlo simulation approach. A Monte Carlo simulation consists of three main steps: (i) we generate a set of random samples from the known input distribution; (ii) we apply a physical transformation to each sample; and (iii) we estimate the distribution of the output variable by approximating the histogram of the computed samples. Monte Carlo simulations are often applied in geoscience studies to quantify the propagation of the uncertainty from the input data to the predicted values of a physical model.
In many subsurface modeling problems, we cannot directly measure the properties of interest but can only collect data indirectly related to them. For example, in reservoir modeling, we cannot directly measure porosity far away from the well, but we can acquire seismic data that depend on porosity and other rock and fluid properties. Geophysics generally provides the physical models that link the unknown property, such as porosity, to the measured data, such as seismic velocities. Therefore, the estimation of the unknown model from the measured data is, from the mathematical point of view, an inverse problem.
If mrepresents the unknown physical variables (i.e. the model), drepresents the measurements (i.e. the data), and fis the set of physical equations (i.e. the forward operator) that links the model to the data, then the problem can be formulated as:
(1.46) 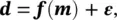
where εis the measurement error associated with the data. The data dcan be a function of time and/or space, or a set of discrete observations. When mand dare vectors of size n mand n d, respectively, then fis a function from 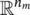 to
to 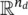 . When mand dare functions, then fis an operator. The operator fcan be a linear or non‐linear system of algebraic equations, ordinary or partial differential equations, or it might involve an algorithm for which there is no explicit analytical formulation. The forward problem is to compute dgiven m. Our focus is on the inverse problem of finding mgiven dand assessing the uncertainty of the predictions. In other words, we aim to predict the posterior distribution of m∣ d.
. When mand dare functions, then fis an operator. The operator fcan be a linear or non‐linear system of algebraic equations, ordinary or partial differential equations, or it might involve an algorithm for which there is no explicit analytical formulation. The forward problem is to compute dgiven m. Our focus is on the inverse problem of finding mgiven dand assessing the uncertainty of the predictions. In other words, we aim to predict the posterior distribution of m∣ d.
In the case of a linear inverse problem with a finite number of measurements 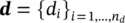 , we can write Eq. (1.46)as a linear system of algebraic equations:
, we can write Eq. (1.46)as a linear system of algebraic equations:
(1.47) 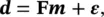
where Fis the matrix of size n d× n massociated with the linear operator f. A common approach to find the solution of the inverse problem associated with Eq. (1.47)is to estimate the model mthat gives the minimum misfit between the data dand the theoretical predictions 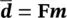 of the forward problem, by minimizing the L2‐norm (also called the Euclidean norm) ‖ r‖ 2of the residuals r= d − Fm:
of the forward problem, by minimizing the L2‐norm (also called the Euclidean norm) ‖ r‖ 2of the residuals r= d − Fm:
(1.48) 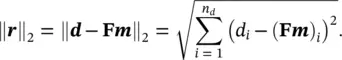
The model m *that minimizes the L2‐norm is called the least‐squares solution because it minimizes the sum of the squares of the differences of measured and predicted data, and it is given by the following equation, generally called the normal equation (Aster et al. 2018):
(1.49) 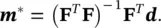
If we consider the data points to be imperfect measurements with random errors, the inverse problem associated with Eq. (1.47)can be seen, from a statistical point of view, as a maximum likelihood estimation problem. Given a model m, we assign to each observation d ia PDF f i( d i∣ m) for i = 1, … , n dand we assume that the observations are independent. The joint probability density of the vector of independent observations dis then:
(1.50) 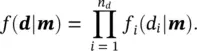
The expression in Eq. (1.50)is generally called likelihood function. In the maximum likelihood estimation, we select the model mthat maximizes the likelihood function. If we assume a discrete linear inverse problem with independent and Gaussian distributed data errors ( 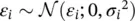 for i = 1, … , n d), then the maximum likelihood solution is equivalent to the least‐squares solution. Indeed, under these assumptions, Eq. (1.50)can be written as:
for i = 1, … , n d), then the maximum likelihood solution is equivalent to the least‐squares solution. Indeed, under these assumptions, Eq. (1.50)can be written as:
Читать дальше

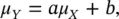
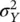 :
: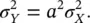
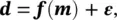
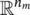 to
to 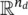 . When mand dare functions, then fis an operator. The operator fcan be a linear or non‐linear system of algebraic equations, ordinary or partial differential equations, or it might involve an algorithm for which there is no explicit analytical formulation. The forward problem is to compute dgiven m. Our focus is on the inverse problem of finding mgiven dand assessing the uncertainty of the predictions. In other words, we aim to predict the posterior distribution of m∣ d.
. When mand dare functions, then fis an operator. The operator fcan be a linear or non‐linear system of algebraic equations, ordinary or partial differential equations, or it might involve an algorithm for which there is no explicit analytical formulation. The forward problem is to compute dgiven m. Our focus is on the inverse problem of finding mgiven dand assessing the uncertainty of the predictions. In other words, we aim to predict the posterior distribution of m∣ d.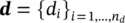 , we can write Eq. (1.46)as a linear system of algebraic equations:
, we can write Eq. (1.46)as a linear system of algebraic equations: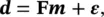
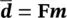 of the forward problem, by minimizing the L2‐norm (also called the Euclidean norm) ‖ r‖ 2of the residuals r= d − Fm:
of the forward problem, by minimizing the L2‐norm (also called the Euclidean norm) ‖ r‖ 2of the residuals r= d − Fm: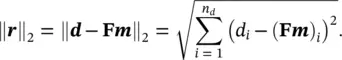
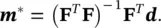
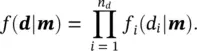
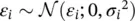 for i = 1, … , n d), then the maximum likelihood solution is equivalent to the least‐squares solution. Indeed, under these assumptions, Eq. (1.50)can be written as:
for i = 1, … , n d), then the maximum likelihood solution is equivalent to the least‐squares solution. Indeed, under these assumptions, Eq. (1.50)can be written as:










