1 ...6 7 8 10 11 12 ...19 Gleichung (1.19)liefert eine Erklärung des Wasserstoffatomemissionsspektrums. Nach (1.19)kann die Energie eines Photons, oder die Energiedifferenz der Atomenergieniveaus, zwischen zwei beliebigen Zuständen n fund n ials
(1.20) 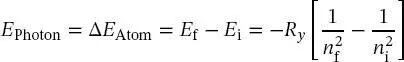
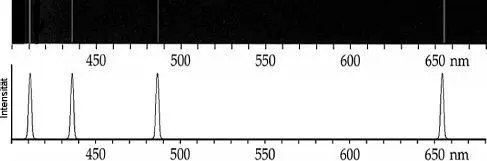
Abb. 1.3Teil des Emissionsspektrums des Wasserstoffatoms im sichtbaren Spektralbereich, hier als Linienspektrum und als Emissionsspektrum dargestellt.
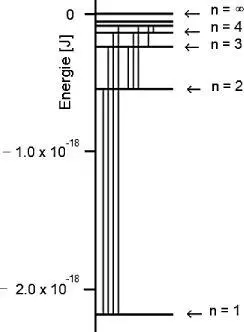
Abb. 1.4Energieniveaudiagramm des Wasserstoffatoms. Übergänge zwischen Energieniveaus sind durch vertikale Linien angedeutet.
geschrieben werden. An dieser Stelle kann ein Beispiel 1.2 angebracht sein, um zu demonstrieren, wie diese empirisch abgeleitete Gleichung die Energie, Wellenlänge und Wellenzahl des von Wasserstoffatomen emittierten Lichts vorhersagt. Dieses Beispiel führt auch ein allgemeines Problem ein, nämlich das von Einheiten. Obwohl es eine internationale Vereinbarung darüber gibt, welche Einheiten (das Système International d’unités oder SI-Einheiten) zur Beschreibung von spektralen Übergängen verwendet werden sollen, besteht das Problem darin, dass sie nur von wenigen Personen verwendet werden. In diesem Buch werden alle Anstrengungen unternommen, SI-Einheiten zu verwenden oder zumindest an die Umrechnung auf andere Einheiten zu erinnern.
Die hier verwendeten Vorzeichenkonventionen ähneln denen in der Thermodynamik, wo ein Prozess mit einem niedrigeren Endenergiezustand als dem des Anfangszustands als ,,exothermer“ Prozess bezeichnet wird, bei dem Wärme oder Energie verloren geht. In Beispiel 1.2 geht die Energie als Photon verloren und wird als Emissionsübergang bezeichnet. Bei der Beschreibung eines Absorptionsprozesses ist die Energiedifferenz des Atoms negativ, Δ E Atom< 0, d. h., das Atom hat Energie gewonnen (,,endothermer“ Prozess in der Thermodynamik). Wenn man dem gleichen Verfahren wie in Beispiel 1.2 folgt, würde dies zu einer negativen Wellenlänge des Photons führen, was natürlich physikalisch bedeutungslos ist, und man muss bedenken, dass das negative negative Δ E Atomdie Absorption eines Photons bedeutet.
Beispiel 1.2: Berechnung von Energie, Frequenz, Wellenlänge und Wellenzahl eines Photons, das von einem Wasserstoffatom emittiert wird, das einen Übergang von n = 6 nach n = 2 durchläuft.
Die Energiedifferenz zwischen den beiden Zuständen des Wasserstoffatoms ist durch
(B1.2-1) 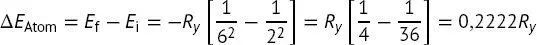
gegeben. Unter Verwendung des oben angegebenen Wertes der Rydberg-Konstante, Ry = 2,179 · 10 −18J, beträgt die Energiedifferenz
(B1.2-2) 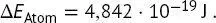
Mit (1.12), Δ E = E Photon= hν = hc/λ , wird die Frequenz ν ermittelt:
(B1.2-3) 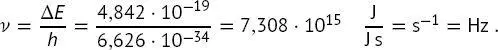
Die Wellenlänge eines solchen Photons ist durch (1.7)gegeben:
(B1.2-4) 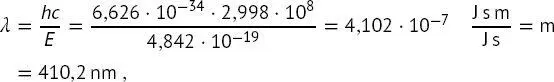
d h. ein Photon im ultravioletten Wellenlängenbereich. Schließlich ist die Wellenzahl dieses Photons
(B1.2-5) 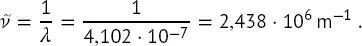
Dies ist ein Fall, in dem die SI-Einheiten selten verwendet werden. Ergebnisse für die Wellenzahl werden gewöhnlich von Spektroskopikern in Einheiten von cm −1angegeben, wobei 1m −1= 10 −2cm −1. Dementsprechend wird das Ergebnis in (B1.2-5)als 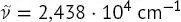 oder ungefähr 24 380 cm −1angegeben.
oder ungefähr 24 380 cm −1angegeben.
Beispiel 1.2 im vorherigen Abschnitt beschreibt einen Emissionsprozess in der Atomspektroskopie , ein Thema, das in diesem Buch nur kurz behandelt wird ( Kap. 9). Die molekulare Spektroskopie ist ein Wissenschaftszweig, in dem die Wechselwirkungen von elektromagnetischer Strahlung und Molekülen untersucht werden, wobei die Moleküle in gequantelten, stationären Energiezuständen vorliegen, die denen, im vorherigen Abschnitt diskutierten ähnlich sind. Diese Energiezustände können entweder auf Übergänge von Elektronen in unterschiedliche Energieniveaus oder auf Schwingungs-, Rotations- oder Spinenergieniveaus zurückzuführen sein. Daher wird die Molekülspektroskopie häufig nach den Wellenlängenbereichen der elektromagnetischen Strahlung (beispielsweise Mikrowellen- oder Infrarotspektroskopie) oder nach Änderungen der Energieniveaus der molekularen Systeme klassifiziert. Dies ist in Tab. 1.1 zusammengefasst, und die Umwandlung von Wellenlängen und Energien wurde in (1.11)– (1.15)diskutiert.
In Tab. 1.1 stehen NMR und EPR für kernmagnetische bzw. elektronenparamagnetische Resonanzspektroskopie. Bei diesen beiden spektroskopischen Methoden hängt die Übergangsenergie eines Protonen- oder Elektronenspins von der angelegten Magnetfeldstärke ab. Alle in Tab. 1.1 aufgeführten Techniken können durch Absorptionsprozesse beschrieben werden, obwohl auch andere Beschreibungen, wie z. B. die Magnetisierung in der NMR, möglich sind. Wie aus Tab. 1.1 hervorgeht, liegen die Photonenenergien zwischen 10 −16und 10 −25J/Photon oder zwischen etwa 10 −4und 10 5kJ/(mol Photonen). Wenn man bedenkt, dass die Bindungsenergie einer typischen chemischen (Einfach-)Bindung etwa 250–400 kJ/mol beträgt, zeigt sich,dass ultraviolette Photonen genügend Energie haben, um chemische Bindungen aufzubrechen oder Moleküle zu ionisieren. In diesem Buch werden aber hauptsächlich energiearme Photonenwechselwirkungen diskutiert, die Übergänge in Spinzuständen, Rotations-, Vibrations- und elektronischen (vibronischen) Energieniveaus verursachen.
Tab. 1.1Photonenenergien und spektroskopische Bereiche a).
| Wellenbereich |
νPhoton |
λPhoton |
EPhoton [J] |
EPhoton [kJ/mol] |
EPhoton [m−1] |
Übergänge |
| Radio |
750 MHz |
0,4m |
5 · 10 −25 |
3 · 10 −4 |
2,5 |
NMR b) |
| Mikrowellen |
3GHz |
10cm |
2 · 10 −24 |
0,001 |
10 |
EPR b) |
| Mikrowellen |
30GHz |
1 cm |
2 · 10 −23 |
0,012 |
100 |
Rotationsanregung |
| Infrarot |
3 · 10 13Hz |
10 μm |
2 · 10 −20 |
12 |
10 5 |
Schwingungsanregung |
| UV/Vis |
10 15Hz |
300 nm |
6 · 10 −19 |
360 |
3 · 10 6 |
Elektronische Anregung |
| Röntgen |
10 18Hz |
0,3 nm |
6 · 10 −16 |
3,6 · 10 5 |
3 · 10 9 |
Röntgenabsorption |
a) Informationen zur Energieumrechnung finden Sie in Anhang A.
Читать дальше

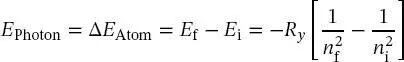


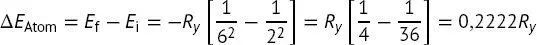
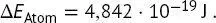
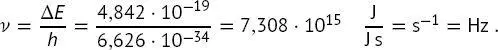
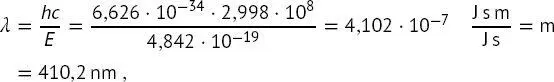
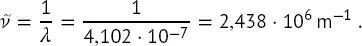
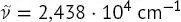 oder ungefähr 24 380 cm −1angegeben.
oder ungefähr 24 380 cm −1angegeben.










