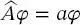1 ...8 9 10 12 13 14 ...19 Das bedeutet, dass die Unsicherheit in der Bestimmung von Impuls und Position immer größer als ist, wobei 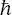 die Planck’sche Konstante geteilt durch 2 π ist. Mathematisch ergibt sich (2.1)aus der Tatsache, dass die Operatoren die für die Definition von Position und Impuls verantwortlich sind, nicht kommutieren; d. h.,
die Planck’sche Konstante geteilt durch 2 π ist. Mathematisch ergibt sich (2.1)aus der Tatsache, dass die Operatoren die für die Definition von Position und Impuls verantwortlich sind, nicht kommutieren; d. h., 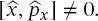 (Dieser Aspekt wird am Ende von Abschn. 2.1ausführlicher behandelt.) Wie wir später sehen werden ( Kap. 5), kann das Unsicherheitsprinzip auch in Bezug auf Energie und Lebensdauer eines spektroskopischen Zustands oder in Bezug auf Frequenz und Zeit einer Welle ausgedrückt werden.
(Dieser Aspekt wird am Ende von Abschn. 2.1ausführlicher behandelt.) Wie wir später sehen werden ( Kap. 5), kann das Unsicherheitsprinzip auch in Bezug auf Energie und Lebensdauer eines spektroskopischen Zustands oder in Bezug auf Frequenz und Zeit einer Welle ausgedrückt werden.
Die Einbeziehung dieser Unsicherheit in das Bild der Bewegung mikroskopischer Teilchen führt zu Diskrepanzen zwischen klassischer Mechanik und Quantenmechanik: Die klassische Physik hat ein deterministisches Ergebnis, das bedeutet, dass Position und Geschwindigkeit (Trajektorie) eines sich bewegenden Körpers bestimmt und mit Sicherheit vorauszusagen ist. Dieses Prinzip gilt zweifellos auf der makroskopischen Skala: Wenn die Position und Flugbahn eines makroskopischen Körpers, beispielsweise des Mondes, bekannt ist, ist es zweifellos möglich, seine Position in sechs Tagen zu berechnen und ein Raumschiff an diese vorhergesagte Position zu senden.
Quantenmechanische Systeme gehorchen dagegen einem probabilistischen Verhalten. Da die Position und der Impuls zu keinem Zeitpunkt gleichzeitig bestimmt werden können, kann die Position (oder der Impuls) auch in der Zukunft nicht genau vorhergesagt werden, sondern nur deren Wahrscheinlichkeit. Dies zeigt sich im Postulat, dass alle gegenwärtigen oder zukünftigen Eigenschaften eines Teilchens durch die Wellenfunktion Ψ ( x,t ) eines Systems gegeben sind. Diese Funktion hängt im Allgemeinen von den räumlichen Koordinaten und der Zeit ab. Somit wird für eine eindimensionale Bewegung (die zuerst erörtert wird) die Wellenfunktion als Ψ ( x, t ) geschrieben. Die Wahrscheinlichkeit, ein quantenmechanisches System zu einem Zeitpunkt an einer bestimmten Position zu finden, ergibt sich aus dem Integral des Quadrats dieser Wellenfunktion: 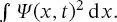 Dies ist in der Tat eines der ,,Postulate“, auf denen die Quantenmechanik basiert ist. Unterschiedliche Autoren zitieren diese Postulate in unterschiedlicher Reihenfolge und schließen eine unterschiedliche Zahl von Postulaten ein, die für die Beschreibung quantenmechanischer Systeme erforderlich ist [1]. Die Quantenmechanik ist insofern ungewöhnlich, weil sie auf diesen Postulaten basiert, während Wissenschaft im Allgemeinen auf Axiomen beruht.
Dies ist in der Tat eines der ,,Postulate“, auf denen die Quantenmechanik basiert ist. Unterschiedliche Autoren zitieren diese Postulate in unterschiedlicher Reihenfolge und schließen eine unterschiedliche Zahl von Postulaten ein, die für die Beschreibung quantenmechanischer Systeme erforderlich ist [1]. Die Quantenmechanik ist insofern ungewöhnlich, weil sie auf diesen Postulaten basiert, während Wissenschaft im Allgemeinen auf Axiomen beruht.
2.1 Postulate der Quantenmechanik
Postulat 1 Der Zustand eines quantenmechanischen Systems ist vollständig durch die Wellenfunktion Ψ ( x, t ) definiert. Das Quadrat dieser Funktion, oder bei komplexer Wellenfunktion das Produkt Ψ *( x, t ) Ψ ( x, t ), integriert über ein Volumenelement 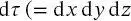 in kartesischen Koordinaten oder
in kartesischen Koordinaten oder 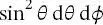 in Polarkoordinaten) gibt die Wahrscheinlichkeit an, ein System im Volumenelement dr zu finden. Hier ist Ψ(x, t) das komplexe Konjugat der Funktion Ψ ( x, t ). Dieses Postulat enthält den Übergang von der deterministischen zur probabilistischen Beschreibung eines quantenmechanischen Systems. Die Wellenfunktionen müssen sich mathematisch gut verhalten, d. h., sie müssen einwertig und stetig sein, mit einer stetigen ersten Ableitung und müssen integrierbar sein (damit sie normiert werden können).
in Polarkoordinaten) gibt die Wahrscheinlichkeit an, ein System im Volumenelement dr zu finden. Hier ist Ψ(x, t) das komplexe Konjugat der Funktion Ψ ( x, t ). Dieses Postulat enthält den Übergang von der deterministischen zur probabilistischen Beschreibung eines quantenmechanischen Systems. Die Wellenfunktionen müssen sich mathematisch gut verhalten, d. h., sie müssen einwertig und stetig sein, mit einer stetigen ersten Ableitung und müssen integrierbar sein (damit sie normiert werden können).
Postulat 2 Der klassische Ausdruck für den linearen Impuls p= m vwird in der Quantenmechanik durch den Differenzialoperator 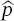 ersetzt, der wie folgt definiert ist:
ersetzt, der wie folgt definiert ist:
(2.2) 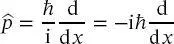
und auf die Wellenfunktion Ψ ( x, t ) angewendet wird. In (2.2)ist i ist die imaginäre Einheit, definiert durch 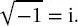 Gleichung (2.2)wird oft als das zentrales Postulat der Quantenmechanik angesehen.
Gleichung (2.2)wird oft als das zentrales Postulat der Quantenmechanik angesehen.
Die Form von (2.2)kann aus Gleichungen der klassischen Wellenmechanik, der De-Broglie-Gleichung (1.10)und der Planck-Gleichung (1.7)plausibel gemachtwerden, aber nicht axiomatisch hergeleitet werden. Erwin Schrödinger hatte die Einsicht und erkannte, dass die Substitution des Impulses durch (2.2)die seit langem bekannten Differenzialgleichungen ergibt, deren Lösungen mit experimentellen Ergebnissen übereinstimmen. In den Schrödinger-Gleichungen, die in den nächsten Kapiteln (für das Wasserstoffatom, die Schwingungen und Rotationen von Molekülen und die molekularen elektronischen Energien) explizit diskutiert werden, wird die klassische kinetische Energie T
(2.3) 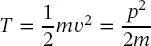
durch
(2.4) 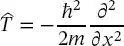
ersetzt. Gleichung (2.4)wurde natürlich durch Einsetzen von (2.2)in (2.3)erhalten.
Die Gesamtenergie eines Systems ergibt sich dann aus der Summe der potenziellen Energie V und der kinetischen Energie T :
(2.5) 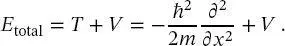
Postulat 3 Alle experimentellen Ergebnisse werden als ,,Observable“ (beobachtbare Größen) bezeichnet, die real (nicht imaginär oder komplex) sein müssen. Alle Observablen sind mit einem quantenmechanischen Operator 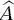 assoziiert (oder sind „Eigenwerte“ von
assoziiert (oder sind „Eigenwerte“ von 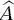 ). Dies wird durch
). Dies wird durch
(2.6) 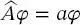
beschrieben, wobei ,, a “ die Eigenwerte sind und die Funktionen φ die entsprechenden Eigenfunktionen. Die Begriffe ,,Operator“, ,,Eigenwerte“ und ,,Eigenfunktio-nen“ stammen aus der linearen Algebra und werden in Abschn. 2.3näher erläutert, wenn das erste Eigenwertproblem, das Teilchen im Kasten, diskutiert wird. Man soll dabei beachten, dass die Eigenfunktionen häufig Polynome sind und jede dieser Eigenfunktionen ihren entsprechenden Eigenwert hat.
Читать дальше

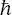 die Planck’sche Konstante geteilt durch 2 π ist. Mathematisch ergibt sich (2.1)aus der Tatsache, dass die Operatoren die für die Definition von Position und Impuls verantwortlich sind, nicht kommutieren; d. h.,
die Planck’sche Konstante geteilt durch 2 π ist. Mathematisch ergibt sich (2.1)aus der Tatsache, dass die Operatoren die für die Definition von Position und Impuls verantwortlich sind, nicht kommutieren; d. h., 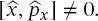 (Dieser Aspekt wird am Ende von Abschn. 2.1ausführlicher behandelt.) Wie wir später sehen werden ( Kap. 5), kann das Unsicherheitsprinzip auch in Bezug auf Energie und Lebensdauer eines spektroskopischen Zustands oder in Bezug auf Frequenz und Zeit einer Welle ausgedrückt werden.
(Dieser Aspekt wird am Ende von Abschn. 2.1ausführlicher behandelt.) Wie wir später sehen werden ( Kap. 5), kann das Unsicherheitsprinzip auch in Bezug auf Energie und Lebensdauer eines spektroskopischen Zustands oder in Bezug auf Frequenz und Zeit einer Welle ausgedrückt werden.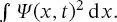 Dies ist in der Tat eines der ,,Postulate“, auf denen die Quantenmechanik basiert ist. Unterschiedliche Autoren zitieren diese Postulate in unterschiedlicher Reihenfolge und schließen eine unterschiedliche Zahl von Postulaten ein, die für die Beschreibung quantenmechanischer Systeme erforderlich ist [1]. Die Quantenmechanik ist insofern ungewöhnlich, weil sie auf diesen Postulaten basiert, während Wissenschaft im Allgemeinen auf Axiomen beruht.
Dies ist in der Tat eines der ,,Postulate“, auf denen die Quantenmechanik basiert ist. Unterschiedliche Autoren zitieren diese Postulate in unterschiedlicher Reihenfolge und schließen eine unterschiedliche Zahl von Postulaten ein, die für die Beschreibung quantenmechanischer Systeme erforderlich ist [1]. Die Quantenmechanik ist insofern ungewöhnlich, weil sie auf diesen Postulaten basiert, während Wissenschaft im Allgemeinen auf Axiomen beruht.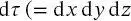 in kartesischen Koordinaten oder
in kartesischen Koordinaten oder 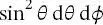 in Polarkoordinaten) gibt die Wahrscheinlichkeit an, ein System im Volumenelement dr zu finden. Hier ist Ψ(x, t) das komplexe Konjugat der Funktion Ψ ( x, t ). Dieses Postulat enthält den Übergang von der deterministischen zur probabilistischen Beschreibung eines quantenmechanischen Systems. Die Wellenfunktionen müssen sich mathematisch gut verhalten, d. h., sie müssen einwertig und stetig sein, mit einer stetigen ersten Ableitung und müssen integrierbar sein (damit sie normiert werden können).
in Polarkoordinaten) gibt die Wahrscheinlichkeit an, ein System im Volumenelement dr zu finden. Hier ist Ψ(x, t) das komplexe Konjugat der Funktion Ψ ( x, t ). Dieses Postulat enthält den Übergang von der deterministischen zur probabilistischen Beschreibung eines quantenmechanischen Systems. Die Wellenfunktionen müssen sich mathematisch gut verhalten, d. h., sie müssen einwertig und stetig sein, mit einer stetigen ersten Ableitung und müssen integrierbar sein (damit sie normiert werden können).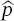 ersetzt, der wie folgt definiert ist:
ersetzt, der wie folgt definiert ist: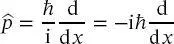
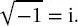 Gleichung (2.2)wird oft als das zentrales Postulat der Quantenmechanik angesehen.
Gleichung (2.2)wird oft als das zentrales Postulat der Quantenmechanik angesehen.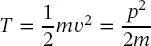
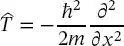
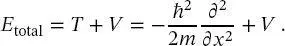
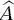 assoziiert (oder sind „Eigenwerte“ von
assoziiert (oder sind „Eigenwerte“ von