In diesem Buch wird der Gesamtenergieoperator durch das Symbol 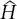 gekennzeichnet und als Hamilton-Operator des Systems bezeichnet. Für die Gesamtenergiegleichung des Systems lautet der Hamilton-Operator dann
gekennzeichnet und als Hamilton-Operator des Systems bezeichnet. Für die Gesamtenergiegleichung des Systems lautet der Hamilton-Operator dann
(2.7) 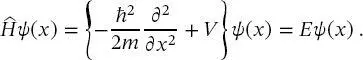
Gleichung (2.7)bedeutet, dass die Energieeigenwerte E durch Anwenden des Operators 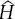 auf die (noch unbekannten) Eigenfunktionen ψ erhalten werden. Es wird hier angenommen, dass sie Funktionen ψ ( x ) zeitunabhängig sind und nur von Raumkoordinaten x abhängen. Die Lösungen der Differenzialgleichungen (2.7)liefert die Eigenfunktionen ψi und ihre zugehörigen Energieeigenwerte Ei .
auf die (noch unbekannten) Eigenfunktionen ψ erhalten werden. Es wird hier angenommen, dass sie Funktionen ψ ( x ) zeitunabhängig sind und nur von Raumkoordinaten x abhängen. Die Lösungen der Differenzialgleichungen (2.7)liefert die Eigenfunktionen ψi und ihre zugehörigen Energieeigenwerte Ei .
Postulat 4 Der Erwartungswert für wiederholte Messungen einer Observablen a , die einem Operator 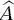 zugeordnet ist, wird durch
zugeordnet ist, wird durch
(2.8) 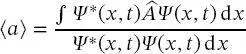
beschrieben. Wenn die Wellenfunktionen Ψ ( x, t ) normalisiert sind, vereinfacht sich (2.7)zu
(2.9) 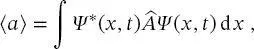
da der Nenner in (2.8)gleich eins ist. Dieser Erwartungswert kann als Durchschnitt vieler unabhängiger Messungen angesehen werden und verkörpert die Wahrscheinlichkeitscharakteristik der Quantenmechanik.
Postulat 5 Die Eigenfunktionen φi , welche die Lösungen der Gleichung 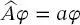 sind, bilden eine vollständige und orthogonale Basis von Funktionen oder, in anderen Worten, definieren einen Vektorraum. Dies wird wiederum in Abschn. 2.3für die Wellenfunktionen des Teilchens im Kasten demonstriert, die alle orthogonal zueinander sind und daher als Einheitsvektoren in einem Vektorraum betrachtet werden können.
sind, bilden eine vollständige und orthogonale Basis von Funktionen oder, in anderen Worten, definieren einen Vektorraum. Dies wird wiederum in Abschn. 2.3für die Wellenfunktionen des Teilchens im Kasten demonstriert, die alle orthogonal zueinander sind und daher als Einheitsvektoren in einem Vektorraum betrachtet werden können.
Wenn die Erwartungswerte 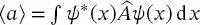 berechnet werden, ist es möglich, dass die Funktionen ψ ( x ) Eigenfunktionen von
berechnet werden, ist es möglich, dass die Funktionen ψ ( x ) Eigenfunktionen von 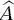 sind oder auch nicht. Dies ist auf die Tatsache zurückzuführen, dass die wirklichen Eigenfunktionen φ(x) einen vollständigen Vektorraum bilden. Funktionen, die nicht Eigenfunktionen von
sind oder auch nicht. Dies ist auf die Tatsache zurückzuführen, dass die wirklichen Eigenfunktionen φ(x) einen vollständigen Vektorraum bilden. Funktionen, die nicht Eigenfunktionen von 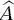 sind, können als lineare Kombinationen der Basisfunktionen φ ( x ) expandiert werden. Somit kann jede beliebige Wellenfunktion ψ eines Systems in Form einer Reihenentwicklung der wahren Eigenfunktionen φ beschrieben werden:
sind, können als lineare Kombinationen der Basisfunktionen φ ( x ) expandiert werden. Somit kann jede beliebige Wellenfunktion ψ eines Systems in Form einer Reihenentwicklung der wahren Eigenfunktionen φ beschrieben werden:
(2.10) 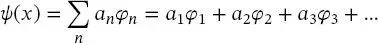
Die Ausdehnungskoeffizienten an zeigen dabei, wie ähnlich die Wellenfunktion der wahren Eigenfunktion des Operators ist.
Postulat 6 Zeitabhängige Systeme werden durch die zeitabhängige Schrödinger-Gleichung beschrieben
(2.11) 
wo die zeitabhängigen Wellenfunktionen das Produkt des zeitunabhängigen Teils, ψ ( x ), und einer Zeitentwicklung ist:
(2.12) 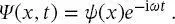
Wir werden der zeitabhängigen Schrödinger-Gleichung hauptsächlich bei Prozessen begegnen, in denen molekulare Systeme durch elektromagnetische Strahlung gestört werden (d. h. in der Spektroskopie). Dabei müssen wir den Formalismus entwickeln, der vorhersagt, ob die einfallende Strahlung einen Übergang zwischen zwei stationären Zuständen im Molekül mit Energiedifferenz 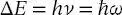 bewirkt oder nicht.
bewirkt oder nicht.
Als Nächstes wird ein einfaches Operator-Eigenwert-Beispiel vorgestellt, um einige der mathematischen Aspekte zu veranschaulichen.
Beispiel 2.1: Operator-Eigenwert-Problem
Es soll gezeigt werden, dass die Funktion 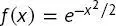 eine Eigenfunktion des Operators
eine Eigenfunktion des Operators 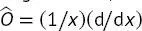 ist, oder in anderen Worten, dass
ist, oder in anderen Worten, dass 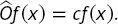
Lösung:
(B2.1-1) 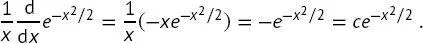
Die Funktion 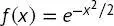 ist eine Eigenfunktion des Operators. Der Eigenwert ist c = −1.
ist eine Eigenfunktion des Operators. Der Eigenwert ist c = −1.
Postulat 7 In Atomen mit mehr als einem Elektron können keine zwei Elektronen identisch die gleichen Quantenzahlen haben. Dieses Postulat ist als Pauli-Ausschließungsprinzip bekannt. Es wird auch wie folgt formuliert: Die Produktwellenfunktion für alle Elektronen in einem Atom muss in Bezug auf den Austausch zweier Elektronen antisymmetrisch sein. Dieses Postulat führt zur Formulierung der Produktwellenfunktion in Form von Slater-Determinanten (siehe Abschn. 9.2) in Mehrelektronensystemen. Der Wert einer Determinante ist null, wenn zwei Zeilen oder zwei Spalten gleich sind. Ein atomares System, in dem Elektronen genau die gleichen vier Quantenzahlen haben, hätte also eine undefinierte Produktwellenfunktion. Darüber hinaus führt der Austausch von zwei Zeilen (oder Spalten) zu einem Vorzeichenwechsel des Wertes der Determinante. Diese letzte Aussage impliziert die antisymmetrische Eigenschaft der Produktwellenfunktion, die beim Austausch zweier Elektronen ihr Vorzeichen ändert.
Читать дальше

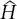 gekennzeichnet und als Hamilton-Operator des Systems bezeichnet. Für die Gesamtenergiegleichung des Systems lautet der Hamilton-Operator dann
gekennzeichnet und als Hamilton-Operator des Systems bezeichnet. Für die Gesamtenergiegleichung des Systems lautet der Hamilton-Operator dann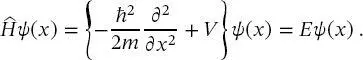
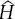 auf die (noch unbekannten) Eigenfunktionen ψ erhalten werden. Es wird hier angenommen, dass sie Funktionen ψ ( x ) zeitunabhängig sind und nur von Raumkoordinaten x abhängen. Die Lösungen der Differenzialgleichungen (2.7)liefert die Eigenfunktionen ψi und ihre zugehörigen Energieeigenwerte Ei .
auf die (noch unbekannten) Eigenfunktionen ψ erhalten werden. Es wird hier angenommen, dass sie Funktionen ψ ( x ) zeitunabhängig sind und nur von Raumkoordinaten x abhängen. Die Lösungen der Differenzialgleichungen (2.7)liefert die Eigenfunktionen ψi und ihre zugehörigen Energieeigenwerte Ei .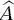 zugeordnet ist, wird durch
zugeordnet ist, wird durch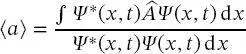
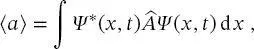
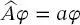 sind, bilden eine vollständige und orthogonale Basis von Funktionen oder, in anderen Worten, definieren einen Vektorraum. Dies wird wiederum in Abschn. 2.3für die Wellenfunktionen des Teilchens im Kasten demonstriert, die alle orthogonal zueinander sind und daher als Einheitsvektoren in einem Vektorraum betrachtet werden können.
sind, bilden eine vollständige und orthogonale Basis von Funktionen oder, in anderen Worten, definieren einen Vektorraum. Dies wird wiederum in Abschn. 2.3für die Wellenfunktionen des Teilchens im Kasten demonstriert, die alle orthogonal zueinander sind und daher als Einheitsvektoren in einem Vektorraum betrachtet werden können.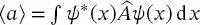 berechnet werden, ist es möglich, dass die Funktionen ψ ( x ) Eigenfunktionen von
berechnet werden, ist es möglich, dass die Funktionen ψ ( x ) Eigenfunktionen von 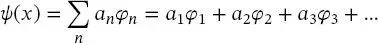

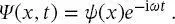
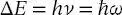 bewirkt oder nicht.
bewirkt oder nicht.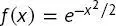 eine Eigenfunktion des Operators
eine Eigenfunktion des Operators 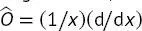 ist, oder in anderen Worten, dass
ist, oder in anderen Worten, dass 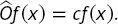
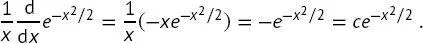
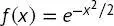 ist eine Eigenfunktion des Operators. Der Eigenwert ist c = −1.
ist eine Eigenfunktion des Operators. Der Eigenwert ist c = −1.










