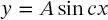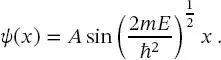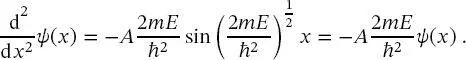Aufgrund der Schwierigkeiten beim Lösen von Gleichungen wie (2.15)und (2.16)wird für das erste Beispiel eines quantenmechanischen Systems eine viel einfachere potenzielle Energiefunktion verwendet, was zu dem bekannten ,,Teilchen-im-Kasten“-Modell führt. Hier wird die Potenzialfunktion einfach durch einen rechteckigen Kasten angenähert. Das Teilchen im Kasten (TiK) ist ein künstliches Beispiel, aber es ist pädagogisch äußerst nützlich und bietet einfache Differenzialgleichungen sowie reale physikalische Anwendungen, siehe Abschn. 2.5.
2.3 Demonstration der quantenmechanischen Prinzipien für ein einfaches, eindimensionales Ein-Elektronen-Modellsystem: Das Teilchen im Kasten
Wirkliche quantenmechanische Systeme neigen dazu, mathematisch ziemlich kompliziert zu sein, aufgrund der Komplexität der im vorherigen Abschnitt erwähnten Differenzialgleichungen. Daher wird hier ein einfaches Modellsystem vorgestellt, um die in den Abschn. 2.1und 2.2 aufgeführten Prinzipien der Quantenmechanik zu veranschaulichen. Dieses Modellsystem ist das sogenannte Teilchen im Kasten (im Folgenden als ,,TiK“ bezeichnet), bei dem der Ausdruck für die potenzielle Energie sehr vereinfacht ist, das aber trotzdem weitreichende Analogien zu wirklichen Systemen aufweist. Dieses Modell ist sehr lehrreich, da es detailliert zeigt, wie der quantenmechanische Formalismus in einer Situation funktioniert, die ausreichend einfach ist, um die Berechnungen schrittweise durchzuführen. Gleichzeitig liefert es Ergebnisse, die den Ergebnissen eines wirklichen Systems sehr ähnlich sind. Dies wird später durch den Vergleich der Symmetrie (Parität) der TiK-Wellenfunktionen mit denen des harmonischen Oszillators ( Kap. 4) veranschaulicht.
Definition des Modellsystems
Das TiK-Modell geht davon aus, dass ein Teilchen, beispielsweise ein Elektron, in ein potenzielles Energiefeld eingebracht wird, das aus zwei unendlich hohen Wänden gebildet wird (siehe Abb. 2.2). Diese Begrenzung (der „Kasten“) hat für 0 ≤ x ≤ L die potenzielle Energie null, wobei L die Länge des Kastens ist. Außerhalb des Kastens, d. h. für x < 0 und für x > L, wird angenommen, dass die potenzielle Energie unendlich ist. Sobald sich das Elektron in der Box befindet, hat es keine Chance zu entkommen, und man weiß mit Sicherheit, dass sich das Elektron in dem Kasten befindet.
Wie bereits erwähnt, wird die Gesamtenergie als die Summe der kinetischen und potenziellen Energie T und V geschrieben:
(2.17) 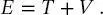
Nach wie vor wird die kinetische Energie des Teilchens als
(2.3) 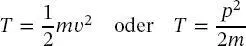
angegeben, wobei m die Masse des Elektrons ist. Ersetzt man den klassischen Impuls in (1.14)durch den quantenmechanischen Impulsoperator,
(2.2) 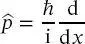
kann der kinetische Energieoperator als
(2.4) 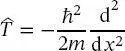
geschrieben werden. Die potenzielle Energie in der Box ist null; somit ist die Gesamtenergie des Teilchens innerhalb des Kastens
(2.18) 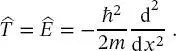
Da die potenzielle Energie außerhalb des Kastens unendlich hoch ist, kann sich das Elektron dort nicht befinden, und die Diskussion wird sich fortan mit dem Inneren des Kastens befassen. Somit kann man den gesamten Hamilton-Operator des Systems als
(2.19) 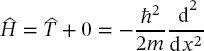
angeben. Im Format der linearen Algebra wird dieses Operator-Eigenvektor-Eigenwert-Problem als
(2.20) 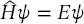
geschrieben. Gleichung (2.20)weist an, den Hamilton-Operator (2.19)auf noch unbekannte Eigenfunktionen anzusetzen, um die gewünschten Energieeigenwerte zu erhalten. Die Eigenfunktionen bilden typischerweise einen n -dimensionalen Vektorraum, in dem die Eigenwerte auf der Diagonale erscheinen. Somit bedeutet (2.20):
(2.21) 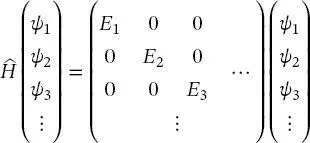
Das heißt, dass der Hamilton-Operator, angesetzt auf die Eigenfunktionen, die Energieeigenwerte 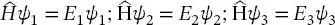 usw. liefert. Dies wird durch Matrixmultiplikation in (2.21)erhalten.
usw. liefert. Dies wird durch Matrixmultiplikation in (2.21)erhalten.
Lösung der Schrödinger-Gleichung für das Teilchen im Kasten
Gleichung (2.19)als kann wie folgt umgeschrieben werden:
(2.22) 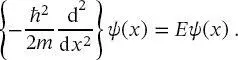
Dies ist eine einfache Differenzialgleichung für die Eigenfunktionen ψ ( x )
(2.23) 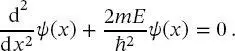
Um (2.23)zu erfüllen, muss die zweite Ableitung der Funktion der ursprünglichen Funktion gleichen, multipliziert mit einer Konstanten. Zum Beispiel könnte die Funktion
(2.24) 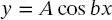
eine Lösung der Differenzialgleichung (2.23)sein, da
(2.25) 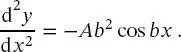
Hier wäre 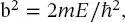 und A ist ein noch nicht definierter Amplitudenfaktor.
und A ist ein noch nicht definierter Amplitudenfaktor.
(2.26) 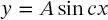
könnte ebenfalls eine Lösung von (2.23)sein sowie eine Summe von (2.24)und (2.26). Aus Gründen, die in Kürze offensichtlich werden,wird (2.26)als Testfunktion zur Erfüllung von (2.23)eingesetzt:
(2.27) 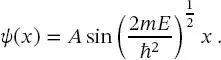
Man erhält damit
(2.28) 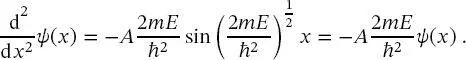
Читать дальше

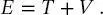
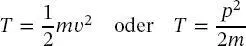
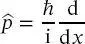
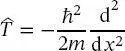
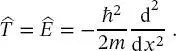
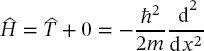
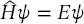
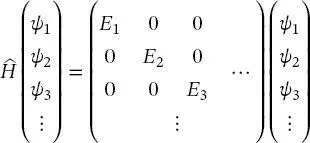
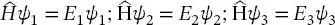 usw. liefert. Dies wird durch Matrixmultiplikation in (2.21)erhalten.
usw. liefert. Dies wird durch Matrixmultiplikation in (2.21)erhalten.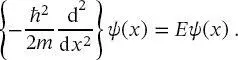
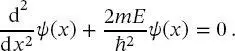
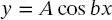
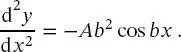
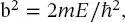 und A ist ein noch nicht definierter Amplitudenfaktor.
und A ist ein noch nicht definierter Amplitudenfaktor.