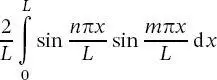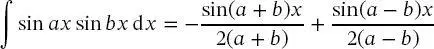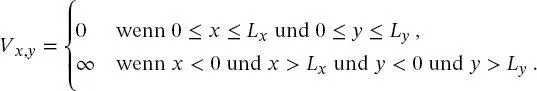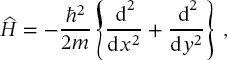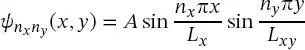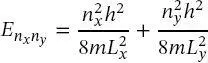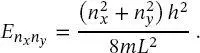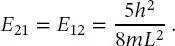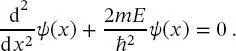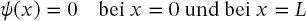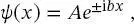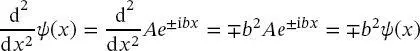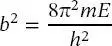(2.40) 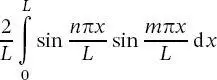
veranschaulicht werden. Dieses Integral kann unter Verwendung der Integralbeziehung
(2.41) 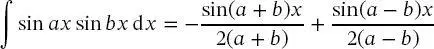
errechnet werden. Für zwei benachbarte Wellenfunktionen, beispielsweise m = 1 und n = 2 oder m = 2 und n = 3, enthält der Zähler des ersten Terms in (2.41)die Sinusfunktion von ungeraden Vielfachen von π , während der Zähler des zweiten Terms die Sinusfunktion von geraden Vielfachen von π enthält. Da die Sinusfunktion von ungeraden und geraden Vielfachen von n null ist, ist das Integral in (2.41)immer null. Dieses Argument gilt für jeden Fall, in dem n ≠ m ist.
Dies kann auch grafisch dargestellt werden, wie in Abb. 2.3b für die ersten beiden TiK-Wellenfunktionen für n = 1 (Kurve a) und m = 2 (Kurve b) gezeigt ist. Das Produkt der beiden Funktionen ergibt Kurve c. Die schattierten Bereiche der Kurve c oberhalb und unterhalb der Abszisse repräsentieren das Integral in (2.40)für n = 1 und m = 2 und sind gleich; daher ist die Fläche unter der Produktkurve c null.
Abbildung 2.2 zeigt auch, dass die Wellenfunktionen für die Zustände mit einer Quantenzahl größer als eins Knotenpunkte oder Punkte ohne Amplitude haben. Dies ist aus dem klassischen Wellenverhalten beispielsweise für eine schwingende Saite bekannt. Die quadrierte Amplitude der Wellenfunktion des TiK bedeutet die Wahrscheinlichkeit, das Elektron aufzufinden; deshalb stellen diese Knotenpunkte Bereiche dar, in denen das Elektron nicht gefunden wird.
1 a) Wie groß ist die Wahrscheinlichkeit P, ein TiK mit n =1 im mittleren Drittel des Kastens zu finden?
2 Was ist P für den gleichen Bereich für ein klassisches Teilchen?
Lösung:
1 a) Die Wahrscheinlichkeit P, ein quantenmechanisches Teilchen oder eine quantenmechanische Welle zu finden, ist durch das Quadrat der Amplitude der Wellenfunktion gegeben, somit:(B2.3-1) Das Integral über die sin2-Funktion wird durch die Beziehung(B2.3-2) erhalten. Damit ist die Wahrscheinlichkeit(B2.3-3)
2 b) Ein klassisches Teilchen würde mit gleicher Wahrscheinlichkeit irgendwo in dem Kasten gefunden werden; somit ist die Wahrscheinlichkeit, es im mittleren Drittel zu finden, nur 1/3. Bitte beachten Sie, dass bei höheren Werten von n die Wahrscheinlichkeit abnimmt, dass das Elektron im mittleren Drittel gefunden wird.
2.4 Das Teilchen in einem zweidimensionalen Kasten, das ungebundene Teilchen und das Teilchen in einem Kasten mit endlichen Energiebarrieren
Teilchen im zweidimensionalen (2-D)-Kasten
Die im vorherigen Abschnitt abgeleiteten Prinzipien können leicht auf einen zweidimensionalen Fall erweitert werden. Hier ist ein Elektron in einem Kasten mit den Dimensionen Lx in der x -Richtung und Ly - in der y -Richtung eingeschlossen. Die potenzielle Energie ist null innerhalb und unendlich außerhalb des Kastens:
(2.42) 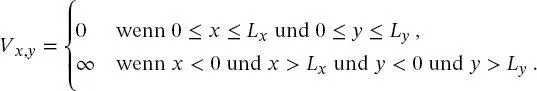
Der Hamilton-Operator für dieses System ist
(2.43) 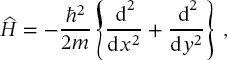
und die gesamte Wellenfunktion ψx y kann als
(2.44) 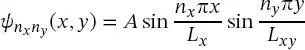
geschrieben werden, wobei A wie zuvor eine Amplitudenkonstante (Normierungskonstante) ist. Die Gesamtenergie des Systems beträgt
(2.45) 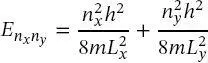
Für ein quadratisches Kästchen mit Lx = Ly = L vereinfacht sich der Ausdruck für die Energie zu:
(2.46) 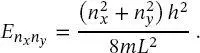
Diese Wellenfunktionen können z. B. für nx = 2 und ny = 1 und nx = 1 und ny = 2 wie in Abb. 2.4 dargestellt werden. Diese Wellenfunktionen repräsentieren eine stehende Welle auf einer quadratischen Trommel. Die Energieeigenwerte für diese beiden Fälle sind gleich:
(2.47) 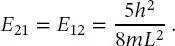
Wenn zwei oder mehr Energieeigenwerte für unterschiedliche Kombinationen von Quantenzahlen gleich sind, werden diese Energiezustände als entartet bezeichnet. Hier erhält man für nx = 2 und ny = 1 und nx = 1 und ny = 2 die gleichen Energieeigenwerte; folglich sind E 21und E 12entartet. Dies ist ein häufiges Vorkommen in der Quantenmechanik, wie wir später in der Diskussion des Wasserstoffatoms ( Kap. 7) sehen werden, wo alle drei 2p-Orbitale, alle fünf 3d-Orbitale und alle sieben 4f-Orbitale entartet sind.
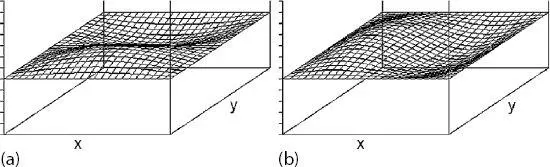
Abb. 2.4Wellenfunktionen für ein TiK in einem zweidimensionalen Kasten (a) nx = 1 und ny = 2(b) nx = 2 und ny = 1 (Quelle: [2]).
Das ungebundene Teilchen
Als Nächstes wird der Fall eines Systems ohne Einschränkung der Randbedingungen (ein ungebundenes Teilchen) diskutiert. Diese Diskussion beginnt mit demselben Hamilton-Operator, der zuvor verwendet wurde:
(2.23) 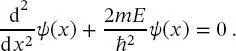
Wenn diese Differenzialgleichung ohne die bisher verwendeten Randbedingungen
(2.29) 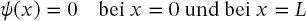
gelöst wird, stellen die neuen Lösungen eine Teilchenwelle dar, die sich entlang der positiven oder negativen x -Richtung bewegt. Die allgemeinste Lösung der Differenzialgleichung (2.23)ist
(2.48) 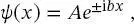
wobei b eine Konstante ist.
Die zweite Ableitung von (2.48)ist durch
(2.49) 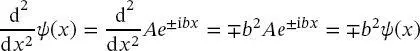
gegeben, wobei
(2.50) 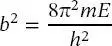
Читать дальше