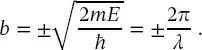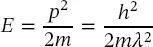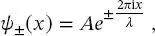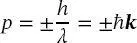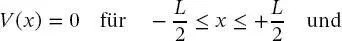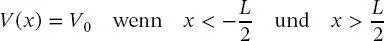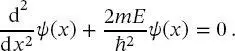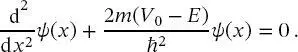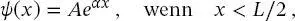Max Diem - Quantenmechanische Grundlagen der Molekülspektroskopie

oder

(2.51)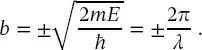

Gleichung (2.51)wurde durch Einsetzen von

(2.52)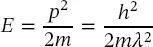

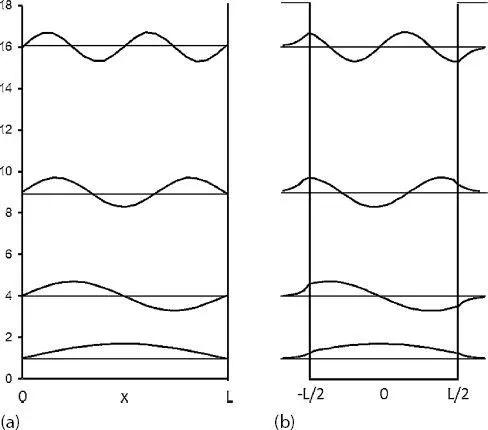
Abb. 2.5Teilchen im Kasten mit (a) unendlich hohen und (b) endlich hohen Energiebarrieren, V 0.

in (2.50)erhalten. Somit kann das ungebundene Teilchen durch eine laufende Welle (im Gegensatz zu einer stehenden Welle) beschrieben werden:

(2.53)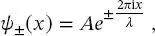

die einen Impuls

(2.54)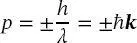

in die positive oder negative x -Richtung trägt. kist dabei der Wellenvektor, der schon vorher definiert wurde (1.6).

Das Teilchen im Kasten mit endlichen Energiebarrieren

Schließlich wird das Teilchen im Kasten mit einer endlichen Energiebarriere V 0qualitativ diskutiert. Dies ist eine Situation, in der das Teilchen außerhalb des Kastens nicht mehr streng verboten ist und zum Konzept des Tunnelns führt, d. h. der Wahrscheinlichkeit, dass das Elektron außerhalb des Kastens gefunden wird. Die Form der Potenzialfunktion ist in Abb. 2.5b dargestellt.

Die potenzielle Energie für diesen Fall wird als

(2.55)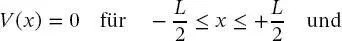

(2.56)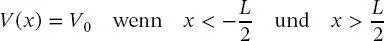

angesetzt. Dabei ist zu beachten, dass die Grenzen des Kastens aus Symmetriegründen von 0 bis L nach — L /2 bis + L /2 verschoben wurden, was in Abschn. 3.2noch einmal behandelt wird. Die Schrödinger-Gleichung besteht aus zwei Teilen: In dem Kasten, in dem die potenzielle Energie null ist, gilt dieselbe Gleichung wie zuvor:

(2.23)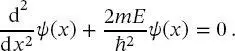

Außerhalb der Box lautet die Schrödinger-Gleichung

(2.57)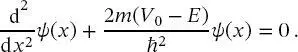

Die Lösungen von (2.57)haben die Form

(2.58)

(2.59)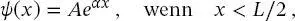

wobei

(2.60)

Für x > L /2 ist ψ ( x ) eine exponentielle Abklingfunktion, und für x < L /2 eine exponentielle Wachstumsfunktion. Dies ist in Abb. 2.5 rechts und links des Kastens dargestellt. Dies ist die Wahrscheinlichkeit, das Elektron außerhalb des Kastens zu finden – ein Vorgang, der als „Tunneln“ bezeichnet wird. Innerhalb des Kastens ähneln die Lösungen von (2.23)den gebundenen Wellenfunktionen des Teilchens im Kasten, mit der Ausnahme, dass die Amplitude an der Grenze nicht mehr null ist, sondern mit der Wellenfunktion außerhalb des Kastens übereinstimmen muss. Dies ist auch in Abb. 2.5b zu sehen. Gebundene Zustände existieren nur für die Energien E ( n ) < V0 ; für E ( n ) > V0 , existiert das Elektron als Wanderwelle, wie zuvor für ungebundene Zustände gezeigt wurde.

Das Konzept des Tunnelns mag zunächst esoterisch erscheinen, hat aber interessante Konsequenzen. Beispielsweise gibt es eine Technik, die als Tunnelelektronenmikroskopie (TEM) bekannt ist, bei der eine sehr scharfe Metallspitze sehr nahe (Bruchteile eines Nanometers) an die Oberfläche der Probe gebracht wird. Die Probe hat ein positives Potenzial gegenüber der Metallspitze. Zwischen der Spitze und dem Analyten wird ein Tunnelstrom beobachtet, der auf das Tunneln von Elektronen von der Spitze zum Analyten zurückzuführen ist. Wenn das Substrat seitlich unter der Spitze bewegt wird, wird die Spitze abgesenkt oder angehoben, um den Tunnelstrom konstant zu halten. Auf diese Weise kann ein ,,Bild“ der Morphologie des Analyten erhalten werden. Das Tunneln kann auch bei bestimmten chemischen Reaktionen eine Rolle spielen, die vom Elektronentransfer von einem Donor zu einem Rezeptor abhängen. Dieser Reaktionen können schneller als die Reaktionsgeschwindigkeit sein, die über die Aktivierungsenergie berechnet wird. Es wird angenommen, dass bei diesen Reaktionen das Elektron sehr schnell vom Donor zum Rezeptor tunnelt. Schließlich spielt das Tunneln eine wichtige Rolle beim letzten Beispiel für ,,wirkliche TiK“ im folgenden Abschnitt.

Übergänge in einem konjugierten Polyen

Obwohl das TiK hier als Modell eingeführt wurde, um quantenmechanische Prinzipien in einem mathematisch behandelbaren System zu demonstrieren, gibt es mehrere physikalische Beispiele, die mit dem TiK-Formalismus angemessen behandelt werden können. Eines davon wird häufig als Experiment im physikalischchemischen Praktikum verwendet [3] und beinhaltet einen konjugierten Farbstoff wie z. B. 1,6-Diphenyl-1,3,5-hexatrien (siehe Abb. 2.6a). In diesem Molekül deutet die Lewis-Struktur auf drei Doppel- und vier Einfachbindungen zwischen den beiden Phenylgruppen hin. Unter dem Gesichtspunkt des TiK-Formalismus kann man das Polyengerüst als die Länge des Kastens betrachten, die durch die gerade Linie zwischen den beiden Phenylgruppen angegeben ist. Die sechs π-Elektronen, die über die gesamte konjugierte Länge delokalisiert sind, sind als sechs TiK-Elektronen zu betrachten, gruppiert als drei Elektronenpaare. Ein π-Bindungsschema ist in Abb. 2.6b dargestellt. Die drei Elektronenpaare würden in diesem Modell die Niveaus n = 1, n = 2 und n = 3 einnehmen, wie durch die Aufwärts- oder Abwärtspfeile in jedem dieser Niveaus angezeigt ist. Das Absorptionsspektrum im sichtbaren Bereich zeigt eine Absorptionsbande, die in dieser Näherung als TiK-Übergang eines Elektrons vom höchsten besetzten Molekülorbital (HOMO) mit n = 3 zum niedrigsten unbesetzten Molekülorbital (LUMO) mit n = 4 zugeordnet wird. Dieser Übergang ist durch den dicken Aufwärtspfeil angezeigt. Im folgenden Beispiel 2.4 wird die Wellenlänge dieser Absorptionsbande berechnet. Dieses Beispiel ist hier vielleicht etwas verfrüht behandelt, da es Aspekte von Übergängen zwischen Energieniveaus, Prinzipien der Bindung von Orbitalen usw. vorstellt, die erst in späteren Kapiteln ausführlicher diskutiert werden. Trotzdem aber zeigt dieses Beispiel gut, dass der TiK-Formalismus auf reale Systeme angewendet werden kann. In einigen Experimenten im Praktikum für physikalische Chemie wird die Abhängigkeit der Absorptionswellenlänge von der Länge des Kastens, d. h. der konjugierten Länge, beschrieben.