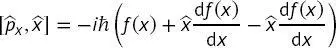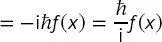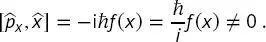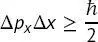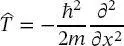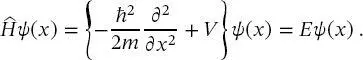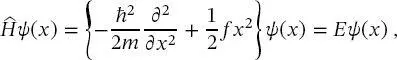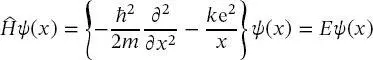Kommutierung von Operatoren: Obwohl es sich hier nicht um ein Postulat der Quantenmechanik handelt (es ist ein genau definiertes mathematische Prinzip), werden hier die Auswirkungen der Kommutierung von Operatoren erörtert. In der Physik möchte man häufig mehrere Größen gleichzeitig bestimmen, beispielsweise die Position und den Impuls eines sich bewegenden Objekts oder die x-, y- und z -Komponente des Drehimpulses. Da das obige Postulat 3 besagt, dass jede beobachtbare Größe einem quantenmechanischen Operator zugeordnet ist, muss der Fall untersucht werden, bei dem gleichzeitig nach den Eigenwerten zweier Operatoren gesucht wird.
Es seien 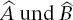 zwei Operatoren, sodass
zwei Operatoren, sodass
(2.13) 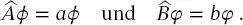
Dabei sind a und b die Eigenwerte und φ und φ die Eigenfunktionen von  bzw.
bzw.  Diese Eigenwerte können dann und nur dann gleichzeitig im selben Vektorraum bestimmt werden, wenn die Operatoren kommutieren, d. h., wenn die Reihenfolge der Anwendung der Operatoren auf die Eigenfunktion unerheblich ist. Der Kommutator zweier Operatoren lautet
Diese Eigenwerte können dann und nur dann gleichzeitig im selben Vektorraum bestimmt werden, wenn die Operatoren kommutieren, d. h., wenn die Reihenfolge der Anwendung der Operatoren auf die Eigenfunktion unerheblich ist. Der Kommutator zweier Operatoren lautet
(2.14) 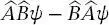
oder abgekürzt 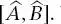 When
When 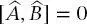 ist, kommutieren die Operatoren, und ihre Eigenwerte können gleichzeitig bestimmt werden. Wenn der Kommutator nicht null ist, können die Eigenwerte nicht gleichzeitig bestimmt werden. Dieser Fall wird in Beispiel 2.2 gezeigt.
ist, kommutieren die Operatoren, und ihre Eigenwerte können gleichzeitig bestimmt werden. Wenn der Kommutator nicht null ist, können die Eigenwerte nicht gleichzeitig bestimmt werden. Dieser Fall wird in Beispiel 2.2 gezeigt.
Der Kommutator 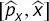 des Impulsoperators
des Impulsoperators 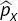 und des Positionsoperators
und des Positionsoperators 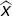 soll bestimmt werden, wenn er auf eine beliebige Funktion f ( x ) angewendet wird.
soll bestimmt werden, wenn er auf eine beliebige Funktion f ( x ) angewendet wird.
Lösung:
(B2.2-1) 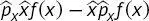
(B2.2-2) 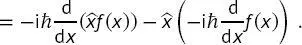
Die Ableitung des Produkts 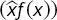 muss anhand der Kettenregel der Differenzierung berechnet werden, somit
muss anhand der Kettenregel der Differenzierung berechnet werden, somit
(B2.2-3) 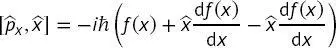
(B2.2-4) 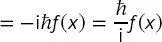
Damit ist der Kommutator
(B2.2-5) 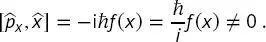
Dies sagt voraus,dass die Position und der Impuls eines sich bewegenden Teilchens nicht gleichzeitig bestimmt werden können. Dies wurde früher in (2.1)als Heisen-berg’sche Unschärferelation
(2.1) 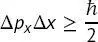
beschrieben. Um die Gleichwertigkeit von (B2.2-5)und (2.1)zu zeigen, müssen die Standardabweichungen von Impuls und Position, σ pund σ x, bestimmt werden, von denen die Unsicherheiten Δ px und Δ x berechnet werden können.
2.2 Die potenzielle Energie und Potenzialfunktionen
Im obigen Postulat 2 wurde die kinetische Energie T durch den Operator
(2.4) 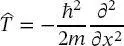
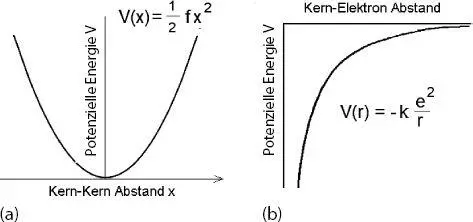
Abb. 2.1Potenzielle Energiefunktionen für (a) Molekülschwingungen und (b) für ein Elektron im elektrostatischen Feld eines Atomkerns. f ist die Kraftkonstante, k die Coulomb’sche Konstante und e die elektronische Ladung.
ersetzt. Die potenzielle Energie V wurde jedoch unverändert belassen, da sie nicht von dem Impuls eines sich bewegenden Teilchens abhängt. Die potenzielle Energie hängt jedoch von den speziellen Wechselwirkungen ab, die das Problem beschreiben, beispielsweise der potenziellen Energie, die ein Elektron im Feld eines Kerns erfährt, oder der potenziellen Energie, die durch eine chemische Bindung zwischen zwei schwingenden Kernen ausgeübt wird. Die Form dieser Potenzialenergiekurven ist in Abb. 2.1 zusammen mit den Potenzialenergiegleichungen dargestellt.
Wenn die Gleichungen für die potenzielle Energie in die Schrödinger-Gleichung
(2.7) 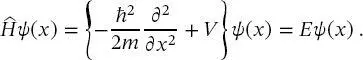
eingesetzt werden, erhält man eine Differenzialgleichung
(2.15) 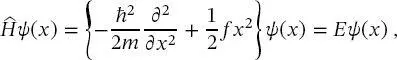
die für die harmonische Schwingung eines zweiatomigen Moleküls gilt, und
(2.16) 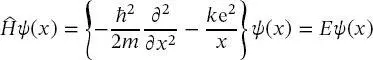
für das Elektron in einem Wasserstoffatom. In (2.15)und (2.16)sind f und k Konstanten, die später eingeführt werden, und ,,e“ ist die elektronische Ladung, e = 1,602 · 10 −19C. Gleichung (2.16)ist nicht exakt korrekt, da die potenzielle Energie eines Elektrons im Feld eines Kerns eine sphärische Funktion ist, die aber in (2.16)und in Abb. 2.1 als eindimensionale Größe dargestellt wird. Außerdem muss die Masse im Nenner des Operators für die kinetische Energie durch die reduzierte Masse ersetzt werden, die später eingeführt wird.
Читать дальше

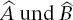 zwei Operatoren, sodass
zwei Operatoren, sodass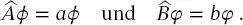
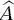 bzw.
bzw. 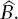 Diese Eigenwerte können dann und nur dann gleichzeitig im selben Vektorraum bestimmt werden, wenn die Operatoren kommutieren, d. h., wenn die Reihenfolge der Anwendung der Operatoren auf die Eigenfunktion unerheblich ist. Der Kommutator zweier Operatoren lautet
Diese Eigenwerte können dann und nur dann gleichzeitig im selben Vektorraum bestimmt werden, wenn die Operatoren kommutieren, d. h., wenn die Reihenfolge der Anwendung der Operatoren auf die Eigenfunktion unerheblich ist. Der Kommutator zweier Operatoren lautet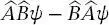
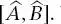 When
When 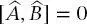 ist, kommutieren die Operatoren, und ihre Eigenwerte können gleichzeitig bestimmt werden. Wenn der Kommutator nicht null ist, können die Eigenwerte nicht gleichzeitig bestimmt werden. Dieser Fall wird in Beispiel 2.2 gezeigt.
ist, kommutieren die Operatoren, und ihre Eigenwerte können gleichzeitig bestimmt werden. Wenn der Kommutator nicht null ist, können die Eigenwerte nicht gleichzeitig bestimmt werden. Dieser Fall wird in Beispiel 2.2 gezeigt.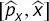 des Impulsoperators
des Impulsoperators 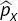 und des Positionsoperators
und des Positionsoperators 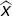 soll bestimmt werden, wenn er auf eine beliebige Funktion f ( x ) angewendet wird.
soll bestimmt werden, wenn er auf eine beliebige Funktion f ( x ) angewendet wird.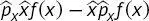
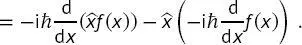
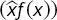 muss anhand der Kettenregel der Differenzierung berechnet werden, somit
muss anhand der Kettenregel der Differenzierung berechnet werden, somit