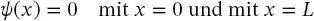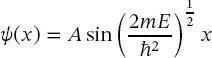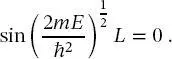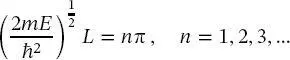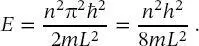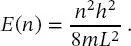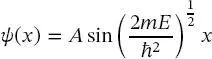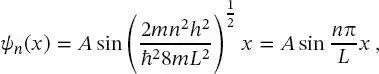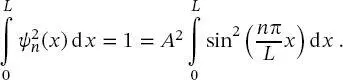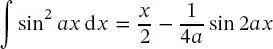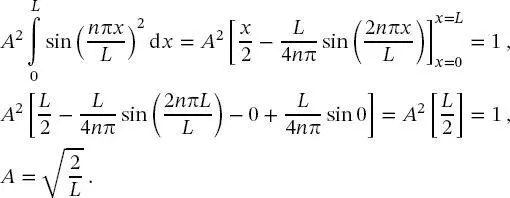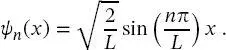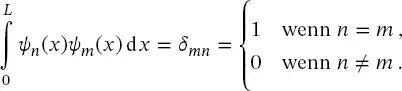Max Diem - Quantenmechanische Grundlagen der Molekülspektroskopie

An dieser Stelle sei darauf hingewiesen, dass die Lösungen einer Differenzialgleichung in hohem Maße von den Randbedingungen abhängen: Die allgemeine Lösung der Differenzialgleichung kann die physikalische Realität des Systems beschreiben oder auch nicht, und es sind die Randbedingungen, die die Lösungen physikalisch sinnvoll machen. Im Falle des TiK werden die Randbedingungen durch eines der Postulate der Quantenmechanik bestimmt, das voraussetzt, dass die Wellenfunktionen stetig sind. Wenn die Wellenfunktion außerhalb des Kastens null ist (da die potenzielle Energie außerhalb des Kastens unendlich hoch ist und daher die Wahrscheinlichkeit null ist, das Teilchen außerhalb des Kastens zu finden), muss die Wellenfunktion innerhalb des Kastens auch an den Grenzen des Kastens null sein. Somit kann man die Randbedingungen für die TiK-Differenzialgleichung als

(2.29)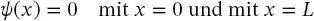

schreiben. Aufgrund dieser Bedingungen wurde die Kosinusfunktion verworfen,die als mögliche Lösungen von (2.23)vorgeschlagen wurde, da die Kosinusfunktion bei x = 0 ungleich null ist. Aufgrund der erforderlichen Kontinuität bei x = L muss der Wert der Funktion

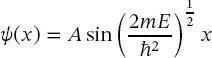
auch bei x = L null sein. Dies kann auf zwei Arten geschehen: Erstens, wenn die Amplitude A null ist. Dieser Fall ist nicht weiter von Interesse, da eine Nullamplitude der Wellenfunktion bedeuten würde, dass sich das Teilchen nicht im Kasten befindet. Die zweite Möglichkeit, dass die Wellenfunktion bei x = L null ist, tritt auf, wenn

(2.30)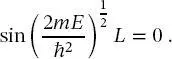

Die Sinusfunktion ist null bei Vielfachen von π und daraus folgt, dass

(2.31)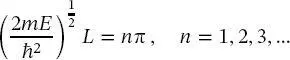

Wenn (2.31)nach E gelöst wird, ergeben sich die Energieeigenwerte

(2.32)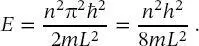

Gleichung (2.32)zeigt, dass die Energieniveaus des TiK gequantelt sind, d. h., die Energie kann keine willkürlichen Werte annehmen, sondern nur Werte von usw. Dies ist das erste Auftreten des Konzepts gequantelter Energieniveaus in einem Modellsystem und stellt einen Schritt dar, der für das Verständnis der Quantenmechanik und der Spektroskopie von enormer Bedeutung ist: Durch Substitution des klassischen Impulses durch den Impulsoperator wurden quantisierte Energieniveaus oder stationäre Zustände erhalten. Diese Quantelung ist eine direkte Folge der Randbedingungen, bei denen die Wellenfunktionen am Rand des Kastens null sein müssen. Da die Energie von dieser Quantenzahl n abhängt, schreibt man (2.32)üblicherweise als

(2.33)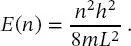

Nach Einsetzen dieser Energieeigenwerte in (2.27)

(2.27)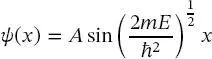

erhält man

(2.34)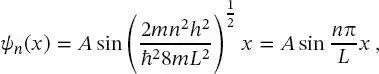

nämlich die Wellenfunktionen für das TiK.

Normierung und Orthogonalität der TiK-Wellenfunktionen

In (2.34)ist ,, A “ ein Amplitudenfaktor, der zu diesem Zeitpunkt noch nicht definiert ist. Um ,, A “ zu bestimmen, argumentiert man wie folgt: Da das Quadrat der Wellenfunktion die Wahrscheinlichkeit ist, das Teilchen zu finden, muss (2.34)eins sein, wenn man sie über die Länge des Kastens integriert, da bekannt ist, dass sich das Teilchen im Kasten befindet. Dies führt zu der Normalisierungsbedingung

(2.35)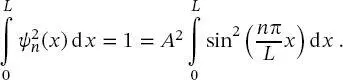

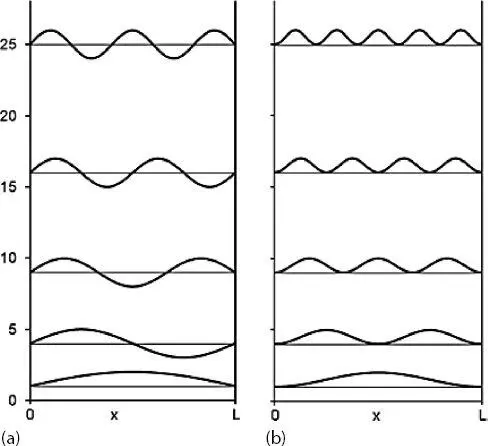
Abb. 2.2(a) Wellenfunktionen für das Teilchen im Kasten für n = 1,2,3,4 und 5, dargestellt mit ihren Energieeigenwerten (in Einheiten von h 2/(8 mL 2)). (b) Quadrat der Wellenfunktionen von (a) (Quelle: [2]).

Mit der Beziehung

(2.36)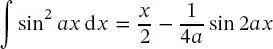

ergibt sich Amplitude A wie folgt:

(2.37)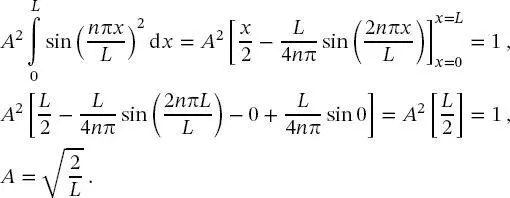

Somit können die normalisierten Wellenfunktionen der stationären Zustände des TiK in endgültiger Form wie folgt geschrieben werden:

(2.38)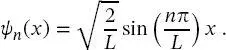

Die (zeitunabhängigen) stationären Wellenfunktionen und Energien sind in Abb. 2.2a dargestellt. Obwohl man diese Wellenfunktionen als zeitunabhängig bezeichnet, können sie als stehende Wellen betrachtet werden, bei denen die Amplituden zwischen den Extremen schwingen (siehe Abb. 2.3) und der Bewegung einer angeregten Saite ähneln. Zeitunabhängigkeit bezieht sich dann auf die Tatsache, dass das System für immer in einem dieser stehenden Wellenmuster verbleibt, bis es durch elektromagnetische Strahlung gestört wird.

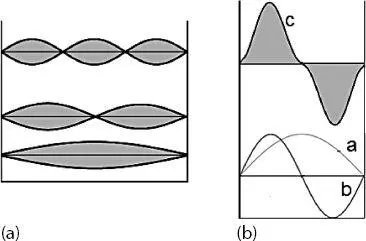
Abb. 2.3(a) Die TiK-Wellenfunktionen aus Abb. 2.2 als stehende Wellen. (b) Veranschaulichung der Orthogonalität der ersten beiden Wellenfunktionen (Quelle: [2]).

Die Wahrscheinlichkeit, das Teilchen an einer bestimmten Position × zu finden, ist in Abb. 2.2b dargestellt. Diese Kurven sind die Quadrate der Wellenfunktionen und zeigen, dass sich bei höheren Niveaus von n die Wahrscheinlichkeit, das Teilchen zu finden, vom Zentrum zur Peripherie des Kastens verschiebt.

Die TiK-Wellenfunktionen bilden einen orthonormalen Vektorraum, d. h.,

(2.39)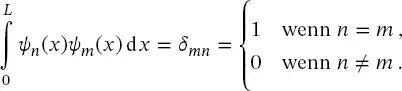

In (2.39)ist δmn das sogenannte Kronecker-Symbol mit dem Wert eins, wenn n = m , und null, wenn n ≠ m . Die Normierung der Wellenfunktionen wurde in (2.36)und (2.37)etabliert. Die Orthogonalität kann durch das Integral