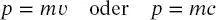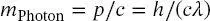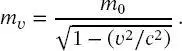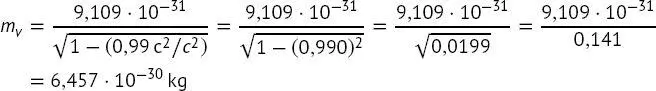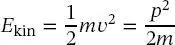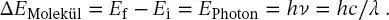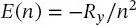Die Welleneigenschaften von Photonen werden durch Beugungsexperimente manifestiert und durch die Maxwell-Gleichung zusammengefasst. Wie bei jeder Wellenausbreitung ist die Lichtgeschwindigkeit c durch die Gleichung
(1.11) 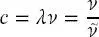
definiert, wobei λ die Wellenlänge (ausgedrückt in m) und ν die Frequenz (ausgedrückt in Hz = s −1) der Welle ist. c hat einen Wert von c = 2,998 · 10 8m/s.
Die Größe  wird als die Wellenzahl der Strahlung (in Einheiten von m −1) bezeichnet, die angibt, wie viele Wellenzyklen pro Längeneinheit auftreten:
wird als die Wellenzahl der Strahlung (in Einheiten von m −1) bezeichnet, die angibt, wie viele Wellenzyklen pro Längeneinheit auftreten:
(1.12) 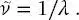
Die (kinetische) Energie eines Photons ist durch
(1.13) 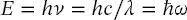
gegeben, wobei 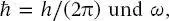 die Winkelfrequenz, durch ω = 2 πν definiert sind.
die Winkelfrequenz, durch ω = 2 πν definiert sind.
Aus der klassischen Definition des Impulses
(1.14) 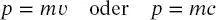
folgt, dass die Photonenmasse durch
(1.15) 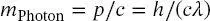
gegeben ist. Dabei soll man beachten, dass sich Photonen nur mit Lichtgeschwindigkeit bewegen können, und dass die Photonenmasse nur bei der Lichtgeschwindigkeit c definiert ist. Daher hat ein Photon die Ruhemasse m 0gleich null.
Materieteilchen haben dagegen eine von null verschiedene Ruhemasse, die üblicherweise als ihre Masse bezeichnet wird. Diese Masse ist jedoch eine Funktion der Geschwindigkeit und sollte als mν bezeichnet werden, definiert durch
(1.16) 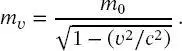
Beispiel 1.1: Berechnung der Masse eines Elektrons, das sich mit 99,0 % der Lichtgeschwindigkeit bewegt. (Solche Geschwindigkeiten können in einem Synchrotron leicht erreicht werden.)
Nach (1.16)ist die Masse mν eines Elektrons bei ν = 0,99 c
(B1.1-1) 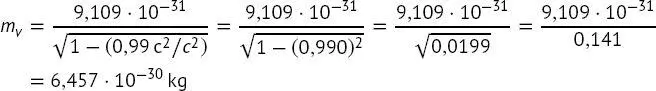
Das Elektron hat bei 99 % der Lichtgeschwindigkeit eine Masse von etwa dem Siebenfachen seiner Ruhemasse.
Gleichung (1.16)zeigt, dass die Masse aller Materieteilchen unendlich wird, wenn sie auf Lichtgeschwindigkeit beschleunigt wird. Ihre kinetische Energie bei der Geschwindigkeit ν (weit entfernt von der Lichtgeschwindigkeit) ist durch den klassischen Ausdruck
(1.17) 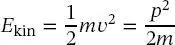
gegeben. Die Diskussion der letzten Absätze zeigt, dass zu Beginn des 20. Jahrhunderts experimentelle Beweise angehäuft wurden, die auf die Notwendigkeit hinwiesen, einige Aspekte der klassischen Physik neu zu definieren. Das nächste dieser Experimente, das zur Formulierung der Quantenmechanik führte, war die Beobachtung von ,,Spektrallinien“ in den Absorptions- und Emissionsspektren des Wasserstoffatoms.
1.4 Absorptions- und Emissionsspektren von Wasserstoffatomen
In den letzten Jahrzehnten des 19. und des ersten Jahrzehnts des 20. Jahrhunderts stellten mehrere Forscher fest, dass Wasserstoffatome, die in Gasentladungslampen erzeugt wurden, Licht in diskreten Farben und nicht in einem breiten Lichtkontinuum (wie in Abb. 1.2a) emittieren. Dies ist in Abb. 1.3 für den ultravioletten und sichtbaren Spektralbereich schematisch dargestellt. Diese Beobachtungen gingen den in den vorangegangenen beiden Abschnitten diskutierten Bemühungen voraus und können daher als am einflussreichsten für die Entwicklung der Verbindung zwischen Spektroskopie und Quantenmechanik angesehen werden.
Diese Experimente zeigten, dass das Wasserstoffatom in bestimmten ,,Energiezuständen“ oder ,,stationären Zuständen“ existieren kann. Diese Zustände können Prozesse durchlaufen, die als ,,Übergänge“ bezeichnet werden. Wenn das Atom einen solchen Übergang von einem höheren oder stärker angeregten Zustand in einen niedrigeren oder weniger angeregten Zustand vollzieht, wird die Energiedifferenz zwischen den Zuständen als Photon mit einer Energie emittiert, die der Energiedifferenz zwischen den beiden Zuständen entspricht:
(1.18) 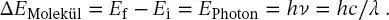
Hier bezeichnet der Index f den endgültigen und der Index i und den anfänglichen (Energie-)Zustand des Atoms (oder Moleküls). Ein solcher Vorgang wird als ,,Emission“ eines Photons bezeichnet. Ebenso ist ein Absorptionsprozess ein Prozess, bei dem das Atom einen Übergang von einem Zustand niedrigerer zu einem Zustand höherer Energie durchläuft, wobei die Energiedifferenz durch ein Photon bereitgestellt wird, das in dem Prozess vernichtet wird. Absorptions- und Emissionsprozesse werden zusammenfassend als Übergänge zwischen stationären Zuständen bezeichnet und stehen in direktem Zusammenhang mit der Vernichtung bzw. Erzeugung eines Photons.
Die Wellenlängen oder Energien der Wasserstoffemissions- oder -absorptionsexperimente wurden durch eine empirische Gleichung angepasst, die als Rydberg-Gleichung bekannt ist und die Energiezustände des Wasserstoffatoms als
(1.19) 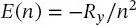
beschreibt. In dieser Gleichung ist n eine ganzzahlige „Quantenzahl“ (> 0) und Ry ist die Rydberg-Konstante ( Ry = 2,179 · 10 −18J). Diese Gleichung impliziert, dass die Energie des Wasserstoffatoms keine willkürlichen Energiewerte annehmen kann, sondern nur ,,gequantelte“ Energieniveaus, E ( n ). Diese Beobachtung führte zu den Vorstellungen von Elektronen in stationären, planetarischen Bahnen um den Kern, die jedoch im Widerspruch zu den zu Beginn dieses Kapitels erörterten Kenntnissen der Elektrodynamik standen.
Das Energieniveaudiagramm nach (1.19)ist in Abb. 1.4 dargestellt. Hier ist die Vorzeichenkonvention wie folgt. Wir nehmen an, dass der niedrigste Energie- oder Grundzustand des Wasserstoffatoms bei n = 1 liegt. Für n = ∞ ist die Energie des Atoms null, da das Elektron nicht mehr mit dem Kern assoziiert ist; daher ist ihre Wechselwirkungsenergie null.
Читать дальше

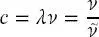
 wird als die Wellenzahl der Strahlung (in Einheiten von m −1) bezeichnet, die angibt, wie viele Wellenzyklen pro Längeneinheit auftreten:
wird als die Wellenzahl der Strahlung (in Einheiten von m −1) bezeichnet, die angibt, wie viele Wellenzyklen pro Längeneinheit auftreten: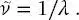
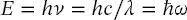
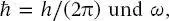 die Winkelfrequenz, durch ω = 2 πν definiert sind.
die Winkelfrequenz, durch ω = 2 πν definiert sind.