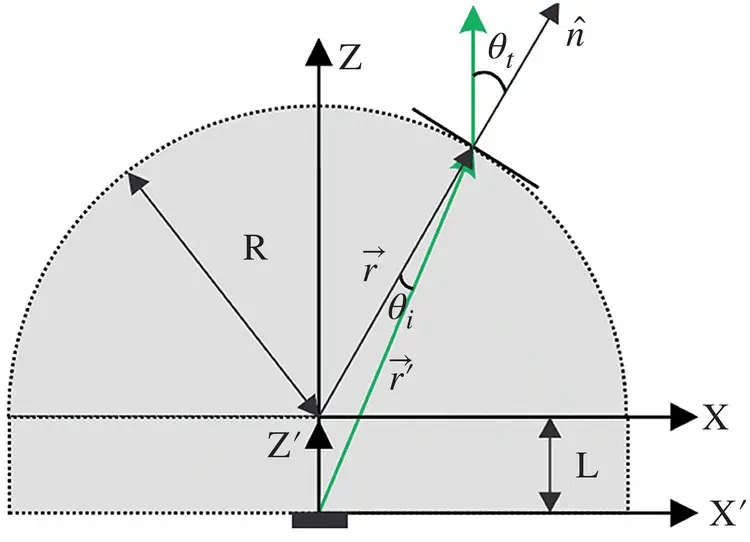
Figure 2.10Sketch of the extended semi‐hemispherical lens antenna parameters.
(2.62) 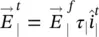
(2.63) 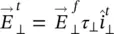
where the τ ‖and τ ⊥are Fresnel transmission coefficients for a dielectric lens of permittivity ε r( 2.27and 2.28). This time the incident angle is evaluated using the normal vector corresponding to the hemispherical lens. The propagation vectors of the incident and transmitted fields are defined as follows:
(2.64) 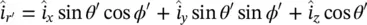
(2.65) 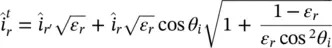
(2.66) 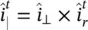
Once the PO surface currents are evaluated via the transmitted fields, one can obtain the far‐field patterns. Those patterns can be obtained using the reference system shown in Figure 2.8, and integrating the PO surface currents over the lens hemispherical surface, as follows:
(2.67) 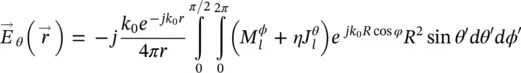
(2.68) 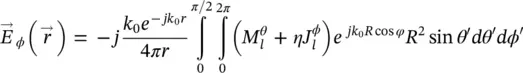
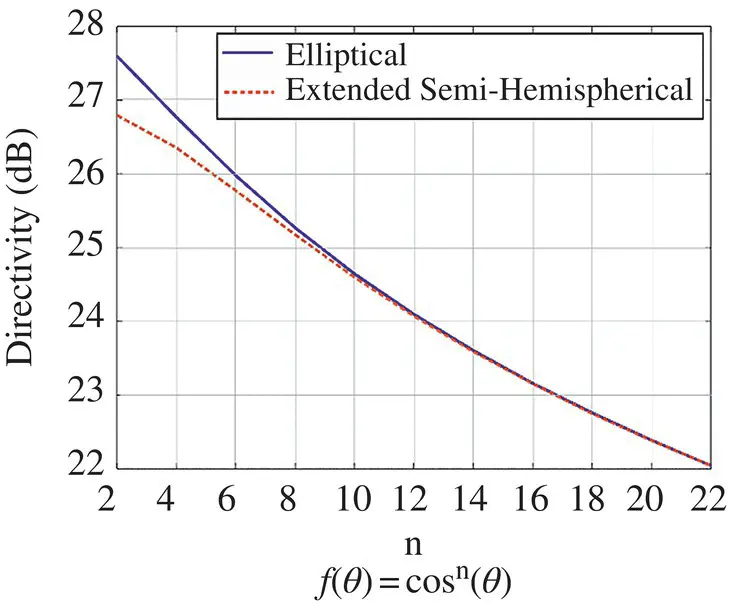
Figure 2.11Directivity of an elliptical lens and an extended hemispherical lens as a function of the feed illumination. A feed illumination of a f ( θ ) = cos n θ is used in the example to illuminate a silicon lens of diameter 7.65 λ and an extended hemispherical lens of L = 0.375.
where R is the radius of the hemisphere of the lens, 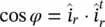 , η . The equivalent magnetic and electric currents are defined as
, η . The equivalent magnetic and electric currents are defined as 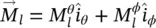 ,
, 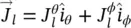 .
.
Figure 2.11shows the directivity of a silicon elliptical lens and a hemispherical lens (i.e. synthesized from the elliptic geometry) as a function of the subtended angle by the feed. As it is shown in the figure, the elliptical lens provides the highest directivity compared to the hemispherical lens, however, the difference is only noticeable when using a feed with low directivity (low n ). As the directivity increases, the performance of the elliptical and extended semi‐hemispherical is equivalent.
2.4 Shallow Lenses Excited by Leaky Wave/Fabry–Perot Feeds
As mentioned in Section 2.3, the amount of energy reflected inside of the lens depends on how the lens feed illuminates the lens surface. The top part of the lens is the most efficient part of the lens since it is where the transmitted energy is the highest, and the least efficient area is the lateral part, leading to high reflected energy. Thus, in order to have a highly efficient lens antenna, we need a feed that illuminates only the top part of the lens, a.k.a. a shallow dielectric lens.
The use of shallow dielectric lenses, as the lens antenna is shown in Figure 2.12, presents great advantages in terms of fabrication and electrical performances at submillimeter‐wave frequencies. Lower cost and better surface accuracies can be achieved when the lens presents a shallow curvature for both silicon micromachining techniques (laser and DRIE photolithography). On the other hand, since the top part of the lens is the most efficient in terms of reflection, we need a feed radiating in an infinite dielectric medium with very large directivity in order to illuminate properly this lens. For example, a lens with a solid angle of 20° will need a cos n θ feed with 19 dB directivity. Generating this type of radiation with low loss is challenging at high frequencies. In Ref. [25], a very directive lens feed, radiating most of the energy well below the air‐dielectric critical angle, with wide bandwidth and a very low‐loss at THz frequencies was proposed using a Fabry–Perot/leaky‐wave concept.
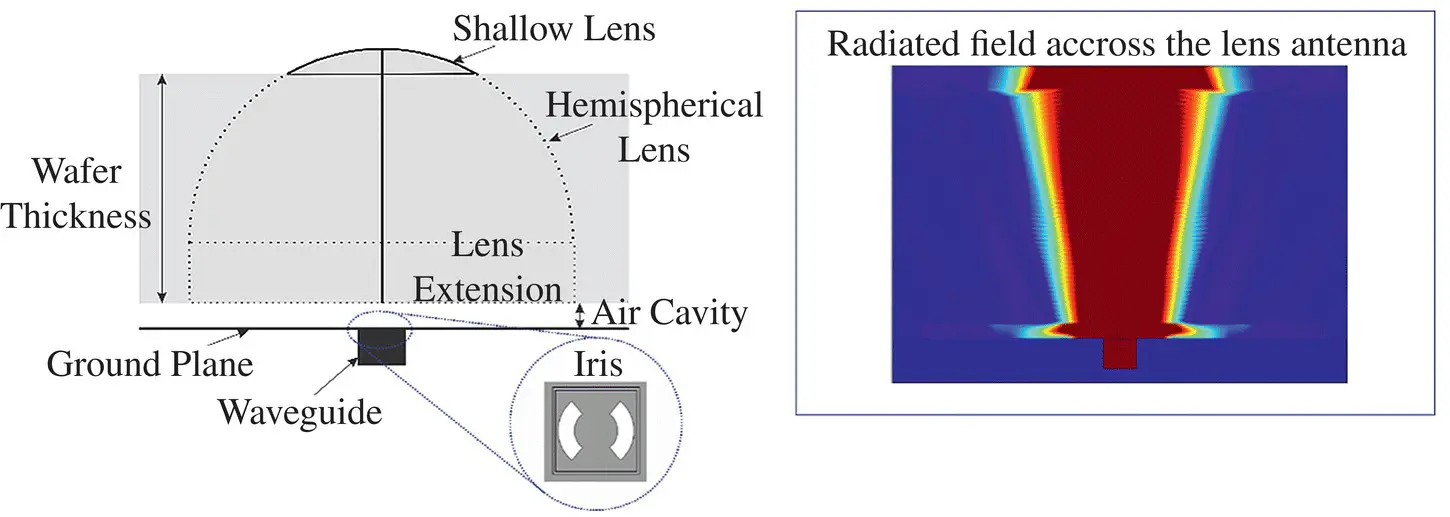
Figure 2.12Sketch of the silicon lens antenna fed by a leaky‐wave feed geometry and its radiated field across the antenna.
Leaky wave antennas (LWAs) [38], also referred as electromagnetic band‐gap (EBG) antennas [39], Fabry–Perot Antennas (FPA) [40] or resonant cavity antennas [41], use a partially transmissive resonant structure that can be made of a thin dielectric superstrate [38] or by using frequency selective surfaces (FSS) [42] to increase the effective area of a small antenna. These antennas are used to achieve high directivity from a point source by the excitation of a pair of nearly degenerated TE 1/ TM 1leaky‐wave modes. These modes propagate in the resonant region by means of multiple reflections between the ground plane and the superstrate, while partially leaking energy into the free space. The amount of energy radiated at each reflection is related to the LW attenuation constant and can be controlled by the FSS sheet‐impedance or the dielectric constant. At the resonant frequency, where the real part and imaginary part of the complex leaky‐wave wavenumber are similar, these antennas radiate a pencil beam. For the air cavity of thickness h 0and dielectric super‐layer of thickness h s, the maximum directivity at broadside is achieved at the resonant condition, i.e. the thickness of the resonant air cavity is h 0= λ 0/2, and that of the super‐layer is 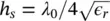 , [38]. Under this condition, the couple of TE / TM leaky‐wave modes can propagate with same phase velocity, creating a nearly uniform phase distribution in the aperture. It has been seen that the generated aperture field is also very well polarized, due to a compensation effect between the TE and TM modal tangential field components [39]. However, this type of LWA also generates an undesired spurious TM 0leaky‐wave mode, conceptually associated with the transverse electromagnetic (TEM) mode of the perfectly conducting walls parallel plate waveguide [43]. This mode radiates near the Brewster angle creating spurious lobes in the E‐plane reducing the beam efficiency. An iris containing a double slot for single‐polarization or two double slots for dual‐polarization will suppress the spurious TM 0mode and provide the matching between the waveguide's fundamental modes and the silicon interface [44].
, [38]. Under this condition, the couple of TE / TM leaky‐wave modes can propagate with same phase velocity, creating a nearly uniform phase distribution in the aperture. It has been seen that the generated aperture field is also very well polarized, due to a compensation effect between the TE and TM modal tangential field components [39]. However, this type of LWA also generates an undesired spurious TM 0leaky‐wave mode, conceptually associated with the transverse electromagnetic (TEM) mode of the perfectly conducting walls parallel plate waveguide [43]. This mode radiates near the Brewster angle creating spurious lobes in the E‐plane reducing the beam efficiency. An iris containing a double slot for single‐polarization or two double slots for dual‐polarization will suppress the spurious TM 0mode and provide the matching between the waveguide's fundamental modes and the silicon interface [44].
Читать дальше


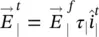
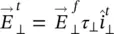
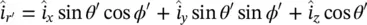
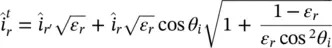
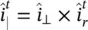
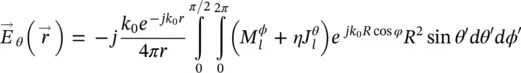
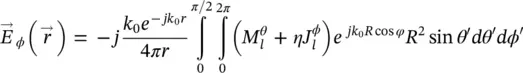

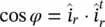 , η . The equivalent magnetic and electric currents are defined as
, η . The equivalent magnetic and electric currents are defined as 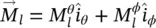 ,
, 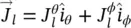 .
.
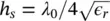 , [38]. Under this condition, the couple of TE / TM leaky‐wave modes can propagate with same phase velocity, creating a nearly uniform phase distribution in the aperture. It has been seen that the generated aperture field is also very well polarized, due to a compensation effect between the TE and TM modal tangential field components [39]. However, this type of LWA also generates an undesired spurious TM 0leaky‐wave mode, conceptually associated with the transverse electromagnetic (TEM) mode of the perfectly conducting walls parallel plate waveguide [43]. This mode radiates near the Brewster angle creating spurious lobes in the E‐plane reducing the beam efficiency. An iris containing a double slot for single‐polarization or two double slots for dual‐polarization will suppress the spurious TM 0mode and provide the matching between the waveguide's fundamental modes and the silicon interface [44].
, [38]. Under this condition, the couple of TE / TM leaky‐wave modes can propagate with same phase velocity, creating a nearly uniform phase distribution in the aperture. It has been seen that the generated aperture field is also very well polarized, due to a compensation effect between the TE and TM modal tangential field components [39]. However, this type of LWA also generates an undesired spurious TM 0leaky‐wave mode, conceptually associated with the transverse electromagnetic (TEM) mode of the perfectly conducting walls parallel plate waveguide [43]. This mode radiates near the Brewster angle creating spurious lobes in the E‐plane reducing the beam efficiency. An iris containing a double slot for single‐polarization or two double slots for dual‐polarization will suppress the spurious TM 0mode and provide the matching between the waveguide's fundamental modes and the silicon interface [44].










