Mittels solcher faktorieller Beschreibungen kann man nicht nur komplexe Variablensysteme auf ihre „Hauptkomponenten“ reduzieren, sondern auch den korrelativen Zusammenhang zwischen verschiedenen Gruppen von Variablen (mit ähnlicher Eigenschaftsbedeutung) bestimmen. (Statistische Verfahren, die auf diesem Prinzip basieren, sind etwa die „Faktorenanalyse“, die „Multivariate Varianzanalyse“, die „Kanonische Korrelation“ oder die „Diskriminanzanalyse“.)
| Abb 3.9
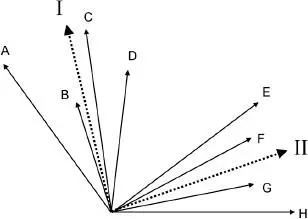
Das Prinzip der „Faktorenanalyse“: Wenn zwischen je zwei dieser acht Variablen der Korrelationskoeffizient berechnet wird und die Variablen in den entsprechenden Winkeln zueinander grafisch dargestellt werden, können Bündel davon durch sogenannte Faktoren (I, II) charakterisiert werden. Die vorliegenden acht Variablen lassen sich relativ gut in nur zwei Dimensionen darstellen, wobei die Länge der Variablenvektoren das Ausmaß ihrer Charakterisierbarkeit durch die beiden senkrecht zueinander stehenden Faktoren widerspiegelt. Im Beispiel könnten die vier Variablen A, B, C und D etwa die Eigenschaften schön, vielfältig, harmonisch und heiter von architektonischen Objekten symbolisieren und aufgrund ihrer vektoriellen Bündelung einen Faktor (I) beschreiben, den man ästhetischer Eindruck nennen könnte.
Eine Erweiterung dieser Verfahren ist die sogenannte „topologische Datenanalyse“ (Wasserman, 2018; Morris, 2015), bei der Daten an empirische Formen oder Strukturen angepasst werden (z.B. Protein-Strukturen, Kommunikationsnetze).
| Inferenzstatistik – schließende und prüfende Statistik |
| 3.6.2 |
Wie mehrfach erwähnt, müssen in der Psychologie Schlussfolgerungen über die allgemeine Gültigkeit von Gesetzen auf Basis von Stichproben gezogen werden. Dies geschieht zumeist unter Verwendung der Wahrscheinlichkeitstheorie, mittels derer man zu bestimmen versucht, ob die in den Daten festgestellten Variablenrelationen nur zufällig oder doch durch Einwirkung eines Gesetzes zustande gekommen sind.
Vereinfacht, aber sehr prägnant kann das Bestreben empirischer Sozialforschung anhand des mathematischen Bayes-Theorems illustriert werden:
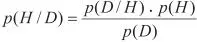
lat. a posteriori: von dem, was nachher kommt
lat. a priori: von vornherein, ohne Einbezug von Erfahrungen
In empirischen Wissenschaften geht es um die Einschätzung der Wahrscheinlichkeit p(H|D) für die Gültigkeit einer Hypothese (H) unter der Bedingung, dass hypothesenbestätigende (oder widerlegende) empirische Daten (D) berücksichtigt werden. Die „Aposteriori-Wahrscheinlichkeit“ p(H|D) für eine Hypothese (d.h. nach Einbezug der Daten) nimmt zu, wenn die „Apriori-Wahrscheinlichkeit“ für die Hypothese p(H) größer wird und/oder wenn die Wahrscheinlichkeit p(D|H) für das Auftreten hypothesenbestätigender Daten ebenfalls zunimmt. Sie nimmt hingegen ab, wenn die hypothesenrelevanten Daten auch unabhängig von der Hypothese häufiger auftreten, das heißt, wenn p(D) größer wird.
Die Plausibilität dieses Ansatzes kann am Beispiel einer medizinischen Diagnose über das Vorliegen einer Covid-19-Infektion illustriert werden: Die Annahme, dass eine Person an Covid-19 (C) erkrankt ist, wenn sie Fieber hat (p(C/F)), stimmt umso eher, (1) je größer p(C) ist, das heißt, je mehr Personen bereits an Covid-19 erkrankt sind (z.B. bei einer Epidemie), (2) je größer p(F|C), die Wahrscheinlichkeit von Fieber bei dieser Viruserkrankung, ist und (3) je kleiner p(F) ist, nämlich die Erwartung des Auftretens von Fieber im Allgemeinen (s. auch 8.5.3; Tschirk, 2019).
Merksatz
Die möglichst stabile Kennzeichnung von Personen oder Personengruppen hinsichtlich wichtiger Eigenschaften, Einstellungen oder Handlungsweisen („Punktschätzungen“) ist eine zentrale sozialwissenschaftliche Zielsetzung.
Eine zentrale sozialwissenschaftliche Zielsetzung besteht in der möglichst stabilen Kennzeichnung von Personen oder Personengruppen hinsichtlich wichtiger Eigenschaften, Einstellungen oder Handlungsweisen („Punktschätzungen“). Da solche Kennwerte immer fehlerbehaftet sind, wird mittels statistischer Techniken ein Vertrauensintervall bzw. Konfidenzintervall für sie bestimmt, innerhalb dessen mit 95%iger (99%iger) Wahrscheinlichkeit der „wahre“ Kennwert vermutet wird.
Es ist leicht einzusehen, dass der Schätzfehler für einen statistischen Kennwert mit zunehmender Größe der Stichprobe immer kleiner wird und schließlich gegen Null geht, wenn alle möglichen Fälle in die Berechnung einbezogen sind ( Abb. 3.10).
| Abb 3.10
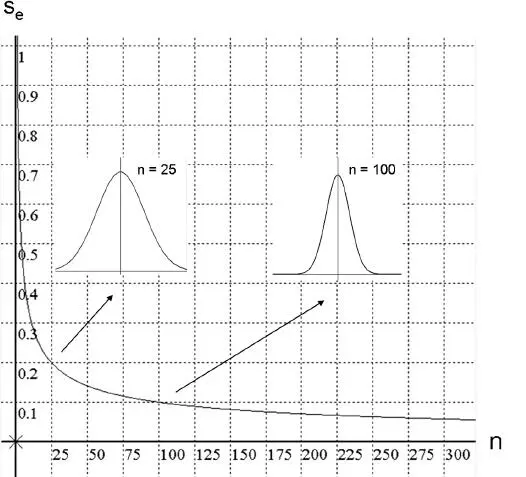
Der Schätzfehler (s e) für die Bestimmung des Mittelwertes einer Population von Fällen aufgrund einer Stichprobe ist eine Funktion der Stichprobenstreuung (s) und des Stichprobenumfanges (n): 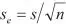 . Je mehr Fälle für eine Schätzung zur Verfügung stehen, desto genauer wird die Vorhersage. Wenn etwa geschätzt werden sollte, wie viel Zeit Arbeiterinnen und Arbeiter durchschnittlich für einen bestimmten Arbeitsgang in einem Produktionsprozess benötigen, dann wird die Schätzung des Mittelwertes anhand einer Stichprobe von 100 Personen eine nur halb so große Fehlerstreuung aufweisen (in Einheiten der Standardabweichung) wie jene auf Basis einer Stichprobe von 25 Personen.
. Je mehr Fälle für eine Schätzung zur Verfügung stehen, desto genauer wird die Vorhersage. Wenn etwa geschätzt werden sollte, wie viel Zeit Arbeiterinnen und Arbeiter durchschnittlich für einen bestimmten Arbeitsgang in einem Produktionsprozess benötigen, dann wird die Schätzung des Mittelwertes anhand einer Stichprobe von 100 Personen eine nur halb so große Fehlerstreuung aufweisen (in Einheiten der Standardabweichung) wie jene auf Basis einer Stichprobe von 25 Personen.
lat. inferre: hineintragen
Die mathematisch begründeten Methoden der Inferenzstatistik sollen also eine Einschätzung erlauben, ob überhaupt und in welchem Ausmaß statistische Resultate von Stichproben auf die jeweilige Population übertragbar sind.
Merksatz
Inferenzstatistische Verfahren zielen darauf ab, den Grad der Allgemeingültigkeit von Gesetzmäßigkeiten zu prüfen, die auf Basis von Stichproben gewonnen werden.
Wenn die Wahrscheinlichkeit dafür, dass bestimmte Variablenrelationen zufällig zu erklären sind, einen vereinbarten Wert unterschreitet (z.B. p = 0,05, p = 0,01 oder p = 0,001), dann spricht man von statistischer Signifikanz des Ergebnisses. Bortz und Döring (1995, 27) definieren statistische Signifikanz als ein „per Konvention festgelegtes Entscheidungskriterium für die vorläufige Annahme von statistischen Populationshypothesen“. Wenn also ein statistisches Ergebnis nur mehr zu 5 % (oder weniger) durch Zufallsprozesse erklärt werden kann, wird es als statistisch signifikant angesehen („überzufällig“ oder „unterzufällig“). Die restliche, für eine Zufallserklärung verbleibende Unsicherheit von 5 % (oder weniger) nennt man Irrtumswahrscheinlichkeit („Fehler 1. Art“, „Alpha-Fehler“), die dazugehörige den Zufallsprozess charakterisierende Annahme (über die Datenverteilung) heißt Nullhypothese.
Da die praktische Bedeutsamkeit eines signifikanten Ergebnisses aber auch von dessen Effektstärke abhängt, müssen abgesehen von der Nullhypothese auch Alternativhypothesen statistisch getestet werden. Das Ausmaß, in dem die Datenverteilungen mit den Vorhersagen einer Alternativhypothese übereinstimmen, wird als Teststärke (engl. power) bezeichnet. Um diese berechnen zu können, ist es nötig, die jeweilige Alternativhypothese zu spezifizieren, indem man die erwartete Effektgröße präzisiert, d.h. schätzt, wie stark die jeweilige unabhängige Variable auf die abhängige Variable einwirken dürfte. Der Vorteil einer solchen Vorgangsweise besteht vor allem darin, dass man nicht nur vage auf „Über- oder Unterzufälligkeit“ von statistischen Ergebnissen schließt, sondern sogar die Wahrscheinlichkeit bestimmen kann, mit der die Daten für die Alternativhypothese sprechen.
Читать дальше


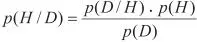

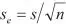 . Je mehr Fälle für eine Schätzung zur Verfügung stehen, desto genauer wird die Vorhersage. Wenn etwa geschätzt werden sollte, wie viel Zeit Arbeiterinnen und Arbeiter durchschnittlich für einen bestimmten Arbeitsgang in einem Produktionsprozess benötigen, dann wird die Schätzung des Mittelwertes anhand einer Stichprobe von 100 Personen eine nur halb so große Fehlerstreuung aufweisen (in Einheiten der Standardabweichung) wie jene auf Basis einer Stichprobe von 25 Personen.
. Je mehr Fälle für eine Schätzung zur Verfügung stehen, desto genauer wird die Vorhersage. Wenn etwa geschätzt werden sollte, wie viel Zeit Arbeiterinnen und Arbeiter durchschnittlich für einen bestimmten Arbeitsgang in einem Produktionsprozess benötigen, dann wird die Schätzung des Mittelwertes anhand einer Stichprobe von 100 Personen eine nur halb so große Fehlerstreuung aufweisen (in Einheiten der Standardabweichung) wie jene auf Basis einer Stichprobe von 25 Personen.










