Abb 3.5 |
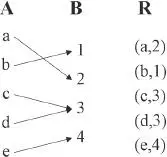
Eine Variablenrelation ist dann eine Variablenfunktion, wenn jeder einzelnen Ausprägung einer Variablen (A) nur genau eine Ausprägung einer anderen Variablen (B) zugeordnet ist.
Als Funktion bezeichnet man eine Relation dann, wenn jeder Ausprägung einer Variablen („Definitionsmenge“) nur genau eine Ausprägung einer anderen Variablen („Funktionsmenge“) zugeordnet ist ( Abb. 3.5). Viele quantitative Funktionen, d.h. Funktionen zwischen Zahlenmengen, können durch einfache Formeln beschrieben werden. Da man in der Psychologie aber neben quantitativen häufig auch nichtquantitative („qualitative“) Merkmale berücksichtigen muss (z.B. Geschlecht, Beruf, Stimmung), werden Variablenbeziehungen im Bedarfsfall auch aussagenlogisch, mengentheoretisch oder tabellarisch dargestellt ( Abb. 3.6).
Wie im vorigen Abschnitt ausgeführt, sind viele Phänomene der Psychologie multikausal oder nur bedingt verursacht, sodass für ihre Aufklärung oft mehrere Variablen einbezogen werden müssen. Relationen zwischen zwei Variablen heißen bivariate, zwischen mehreren Variablen multivariate Variablenrelationen (Box 3.3).
Wenn Variablen quantitativ interpretierbare Ausprägungen haben, kann man sich für die Darstellung von Variablenrelationen auch der analytischen Geometrie bedienen, indem Ausprägungskombinationen als Punkte oder als Vektoren (Pfeile) in einem Raum veranschaulicht werden ( Abb. 3.7).
Da aber in der Empirie nur selten solche Relationen zwischen Variablen vorkommen, die eindeutig mit einer einfachen mathematischen Formel beschreibbar sind (z.B. Junktion, lineare Funktion, Kurve), bedient man sich – wie erwähnt – der Statistik, die auch für fehlerbehaftete, unscharfe oder einander überlagernde Variablenrelationen adäquate Beschreibungsmethoden anbietet. Als eines der größten methodischen Probleme der gegenwärtigen psychologischen Forschung kann gelten, dass die meisten Erklärungsmodelle und Hypothesen weder Multikausalität noch bedingte Kausalität einbeziehen, und daher zu geringe Prognosesicherheit erreichen (Maderthaner, in Vorbereitung).
Box 3.3 | Beispiel für eine multivariate aussagenlogische Beschreibung von Variablenzusammenhängen (mit Multikausalität und bedingter Kausalität)
Inhaltliche Aussage (aus der Sozialpsychologie):
Kinder, die früher an Modellpersonen beobachten konnten, dass sich Aggression „lohnt“ (L), oder solche, die gerade von einem anderen Kind frustriert (F) wurden, tendieren diesem gegenüber zu aggressivem Verhalten (A), wenn dieses eher als wehrlos (W) empfunden wird, wenn ihm gegenüber keine moralischen Hemmungen (M) bestehen und wenn im Moment keine Strafdrohung (S) von Aufsichtspersonen für aggressive Reaktionen zu erwarten ist.
Aussagenlogische Form: ((L ∨ F) ∧ W ∧ ¬ M ∧ ¬ S) ⟶ A
(Zur Bedeutung der Symbole siehe Abb. 3.6; ¬: Negation)
| Abb 3.6
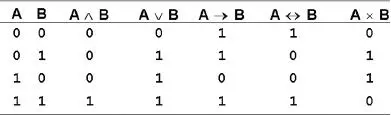
Zweistellige Aussagenrelationen („Junktionen“), wie etwa Konjunktion (∧: „A und B“), Adjunktion (∨: „A oder B“), Implikation (⟶: „wenn A, dann B“) oder Bijunktion (⟷: „wenn A, dann B und umgekehrt“) kennzeichnen durch ihre „Wahrheitswerte“ jene Paare von Ausprägungen der Variablen A und B (1, wenn gegeben, und 0, wenn nicht gegeben), die im Sinne der Relation auftreten können.
| 3.6 | |
Beschreibende und hypothesenprüfende Statistik |
Merksatz
Mittels der Statistik als Hilfswissenschaft werden in der Psychologie verfügbare Daten beschrieben und auf vorhandene Gesetzmäßigkeiten untersucht.
Die Statistik (engl. statistics) fungiert innerhalb der Psychologie als Hilfswissenschaft zur Auffindung und Beschreibung von nichtdeterministischen Gesetzen (Relationen). “Statistics is a set of concepts, rules and methods for (1) collecting data, (2) analyzing data, and (3) drawing conclusions from data” (Iversen & Gergen, 1997, 4). Wenn in der Nachrichtentechnik damit gerechnet wird, dass elektronische Signale von Störungen überlagert werden, dann sendet man gleiche Signale mehrmals hintereinander, um beim Empfang auf Basis ihres Mittelwerts (Durchschnitt) auf das ursprüngliche „wahre“ Signal schließen zu können. Nach dem gleichen Prinzip werden in der Psychologie wiederholt oder simultan Daten über psychische Abläufe, Einstellungen oder Fähigkeiten gesammelt, um daraus Schätzungen über die untersuchten Phänomene ableiten zu können. Die (klassische) Testtheorie postuliert diesem Prinzip gemäß, dass sich jeder Messwert (z.B. eine physiologische Ableitung, eine Fragebogenantwort, eine Prozentschätzung) aus einem wahren Wert - und einem zufälligen Fehlerwert zusammensetzt und dass sich Fehlerüberlagerungen durch Heranziehung mehrerer Messwerte des gleichen Ereignisses „ausmitteln“ lassen.
| Abb 3.7
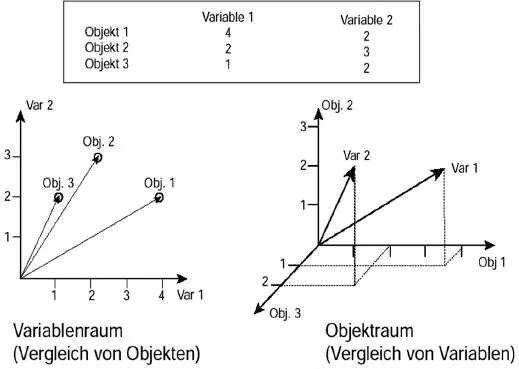
Ähnlich wie physikalische Objekte in einem (euklidischen) Raum Positionen einnehmen können, lassen sich auch Fälle als „Datenobjekte“ auffassen und in einen (multidimensionalen) Variablenraum projizieren. Die Datenobjekte sind einander umso näher, je ähnlicher ihre Variablenausprägungen sind. Ebenso lässt sich die Ähnlichkeit von Variablen in Objekträumen abbilden. Im Beispiel sind drei Objekte (z.B. Personen) im Zweivariablenraum (z.B. Gewicht und Größe) dargestellt und daneben die gleichen Variablen im Dreiobjekteraum.
| 3.6.1 | |
Deskriptivstatistik – beschreibende Statistik |
Die deskriptive Statistik bietet charakteristische, formelhafte Beschreibungen oder grafische Darstellungen für eine große Zahl von Fällen, Variablen oder Variablenrelationen an. Wie schon erwähnt ( Abb. 3.7), werden Fälle als Punkte in einem multidimensionalen Raum von Variablen gedacht, und ihre Verteilung wird durch statistische Kennwerte bzw. Statistiken näher charakterisiert. Eine Voraussetzung für eine solche Darstellung von Variablen (sowie ihres Einbezugs in komplexe statistische Auswertungsverfahren) ist, dass sie quantitativ interpretierbar sind, d.h., dass ihre Ausprägungen unterschiedliche Quantitäten einer Eigenschaft oder eines Merkmals von Fällen kennzeichnen (Backhaus et al., 2003).
Um die quantitative Bedeutung der Ausprägungen von Variablen einzustufen, werden diese hinsichtlich ihrer Skalenqualität, d.h. nach Skalenniveau bzw. Messniveau, differenziert:
1. Nominalskala: Wenn eine Variable nur dieses Skalenniveau zugeschrieben bekommt, sind ihre Ausprägungen (Zahlenwerte) im Sinne von Klassifikationen zu verstehen. Es handelt sich also um Variablen, die („qualitative“) Eigenschaften, wie etwa Geschlecht, Beruf, Nationalität oder Haarfarbe, kennzeichnen.
2. Ordinalskala (Rangskala): Die Werte von Variablen mit ordinaler Skalenqualität gestatten nicht mehr bloß die Unterscheidung zwischen gleich- und ungleichartig, sondern erlauben zusätzlich die Erstellung einer quantitativ begründeten Rangreihe der Variablenausprägungen. Typische Ordinalvariablen sind Listen von Schulnoten oder Rangreihungen bei Wettbewerben.
Merksatz
Die quantitative Interpretierbarkeit von empirischen Variablen bzw. der durch sie beschriebenen Indikatorausprägungen wird durch die ihnen zugeschriebene Skalenqualität (Messniveau) charakterisiert.
3. Intervallskala: Für Variablen dieses Typs wird angenommen, dass ihre aufeinanderfolgenden Zahlenwerte die Zunahme einer variablenspezifischen Eigenschaftsquantität immer um den gleichen Betrag symbolisieren (der Quantitätszuwachs von 1 auf 2 ist der gleiche wie etwa von 4 auf 5). In der Psychologie erwartet man zumindest Intervallskalenniveau von all jenen Variablen, die quantitative Abstufungen von individuellen Leistungspotenzialen (z.B. Konzentration, Intelligenz) oder von psychischen Dispositionen (z.B. Einstellungen, Persönlichkeitsdimensionen) zum Ausdruck bringen wollen.
Читать дальше















