TEORIA D’AUTÒMATS
I LLENGUATGES FORMALS
Educació. Materials 75
Francesc J. Ferri
TEORIA D’AUTOMATSI LLENGUATGES FORMALS
UNIVERSITAT DE VALÈNCIA
2004
Col•lecció: Educació. Materials
Director de la col•lecció: Guillermo Quintas Alonso

Aquesta publicació no pot ser reproduïda, ni totalment ni parcialment, ni enregistrada en, o transmesa per, un sistema de recuperació d’informació, en cap forma ni per cap mitjà, sia fotomecànic, fotoquímic, electrònic, per fotocòpia o per qualsevol altre, sense el permís previ de l’editorial.
© L’autor, 2004
© D’aquesta edició: Universitat de València, 2004
Coberta:
Disseny: Pere Fuster (Borràs i Talens Assessors SL)
Tractament gràfic: Celso Hernandez de la Figuera
Correcció: Pau Viciano
ISBN: 978-84-370-9383-3
Edició digital
Índex
PRÒLEG
SÍMBOLS UTILITZATS
Capítol 1. Llenguatges formals i computació
1.1 Símbols, cadenes i llenguatges
1.1.1 Operacions amb cadenes
1.1.2 Operacions amb llenguatges
1.2 Generació de llenguatges
1.2.1 La jerarquia de Chomsky
1.2.2 Transformació de gramàtiques
1.2.3 Verificació de gramàtiques
1.3 Acceptació de llenguatges i computabilitat
1.4 Exercicis
Capítol 2. Autòmats finits i conjunts regulars
2.1 Tipus d’autòmats finits
2.1.1 Autòmats indeterministes
2.1.2 Autòmats amb transicions buides
2.2 Autòmats finits i llenguatges regulars
2.2.1 Gramàtica equivalent a un autòmat finit
2.2.2 Autòmat equivalent a una gramàtica regular
2.3 Expressions regulars
2.3.1 Conjunts i expressions regulars
2.3.2 Propietats
2.3.3 Equivalències
2.3.4 Càlcul de l’expressió regular equivalent a un autòmat
2.4 Exercicis
Capítol 3. Propietats dels llenguatges regulars
3.1 Lema del bombament
3.1.1 Demostració de la no-regularitat
3.1.2 Problemes de decisió
3.2 Propietats de clausura
3.3 Teorema de Myhill-Nerode
3.3.1 Congruència associada a un llenguatge
3.3.2 Congruència associada a un autòmat
3.3.3 Una altra condició necessària per a la regularitat
3.3.4 Condició suficient per a la regularitat
3.3.5 Conseqüències i aplicacions
3.4 Minimització d’autòmats
3.4.1 Equivalències entre estats
3.4.2 Autòmat associat a la relació d’equivalència
3.4.3 Mètodes gràfics de càlcul de l’autòmat mínim
3.5 Exercicis
Capítol 4. Gramàtiques incontextuals i autòmats amb pila
4.1 Introducció
4.2 Manipulació de gramàtiques incontextuals
4.2.1 Formes normals de Chomsky i Greibach
4.3 Autòmats amb pila
4.3.1 Criteris d’acceptació
4.3.2 Autòmats deterministes i indeterministes
4.4 Relació entre llenguatges incontextuals i autòmats amb pila
4.4.1 Autòmat amb pila equivalent a una gramàtica incontextual
4.4.2 Gramàtica equivalent a un autòmat amb pila
4.4.3 Diferents tipus de llenguatges incontextuals
4.5 Propietats dels llenguatges incontextuals
4.5.1 Lema del bombament per als llenguatges incontextuals
4.5.2 Propietats de clausura
4.5.3 Problemes de decisió
4.6 El problema de l’anàlisi en llenguatges incontextuals
4.6.1 Anàlisi descendent
4.6.2 Anàlisi ascendent
4.7 Exercicis
Capítol 5. La màquina de Turing
5.1 Definició de la màquina de Turing
5.1.1 La màquina de Turing com a acceptor de llenguatges
5.1.2 La màquina de Turing com a model de computació
5.2 Altres tipus de màquines de Turing
5.2.1 La màquina de Turing multipista i multicinta
5.2.2 La màquina de Turing amb cinta semiinfinita
5.2.3 La màquina de Turing modular
5.2.4 Catàleg de màquines modulars
5.2.5 La màquina de Turing indeterminista
5.3 Classes de llenguatges relacionades amb màquines de Turing
5.3.1 Llenguatges acceptats per màquines de Turing
5.3.2 Llenguatges generats per màquines de Turing
5.3.3 La màquina de Turing i la jerarquia de Chomsky
5.3.4 Codificació de màquines de Turing
5.3.5 La màquina de Turing universal
5.3.6 El llenguatge diagonal
5.4 Exercicis
Capítol 6. Resolubilitat
6.1 Resolució de problemes amb màquines de Turing
6.1.1 Funcions computables
6.1.2 Hipòtesi de Church-Turing
6.1.3 Relació entre llenguatges i problemes
6.2 Problemes resolubles i irresolubles
6.2.1 Reducció de problemes
6.2.2 El problema universal
6.3 Decidibilitat d’algunes propietats dels llenguatges recursivament enumerables
6.3.1 El problema del llenguatge buit
6.3.2 El teorema de Rice
6.4 El problema de la correspondència de Post
6.4.1 Enunciat
6.4.2 El problema de Post és indecidible
6.4.3 Problemes irresolubles sobre gramàtiques incontextuals. ...
6.5 El llenguatge de les computacions d’una màquina
6.5.1 Definició
6.5.2 Aplicacions
6.5.3 Altres problemes irresolubles relacionats amb llenguatges incontextuals
6.6 Exercicis
Capítol 7. Introducció a la 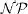 -completesa
-completesa
7.1 Problemes tractables i intractables
7.2 Complexitats associades a màquines de Turing
7.2.1 Complexitat espacial i complexitat temporal
7.2.2 Complexitats i classes de llenguatges
7.3 Problemes 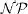 -complets
-complets
7.3.1 Les classes P i 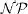
7.3.2 Reducció polinòmica
7.3.3 El teorema de Cook
7.4 Obtenció de problemes 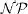 -complets
-complets
7.4.1 El recobriment exacte
7.4.2 El problema de la motxilla
7.5 Exercicis
Bibliografia
Apèndix A. Conceptes matemàtics preliminars
A.1 Conjunts
A.2 Estructures
A.3 Relacions
A.4 Aplicacions
A.5 Conjunts numerables
Apèndix B. Funcions recursives i computabilitat
B.1 Funcions numèriques i simbòliques
B.2 Aproximació recursiva a la computabilitat
B.2.1 Funcions inicials
B.2.2 Funcions recursives primitives
B.2.3 Funcions computables i no recursives primitives
B.2.4 Funcions p-recursives
B.3 Equivalència amb les funcions Turing computables
B.4 Exercicis
Índex analític
PRÒLEG
El present manual pretén donar una introducció als conceptes que constitueixen la base i els fonaments matemàtics de la computació .
A banda de servir de guia d’una assignatura concreta que s’imparteix de forma molt similar en moltes universitats tant a nivell nacional com internacional, l’objectiu principal a l’hora de proposar i desenvolupar aquest estudi ha estat donar una visió personal i adaptada als temps actuals d’una disciplina aparentment allunyada de la pràctica de la informàtica .
Читать дальше



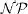 -completesa
-completesa










