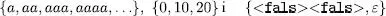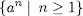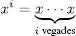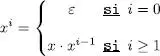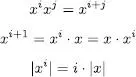Francesc Josep Ferri Rabasa - Teoria d'autòmats i llenguatges formals

Aquest manual té com a objectiu l’estudi dels llenguatges formals, així com dels seus generadors i acceptors, juntament amb l’estreta relació que hi ha entre els llenguatges formals i la teoria de la computació.

Aquest estudi té una formulació matemàtica molt clara a partir del concepte de símbol, les operacions que s’hi poden definir i les seues propietats. Per això, es dedica aquest capítol introductori a donar les definicions bàsiques relacionades amb els diferents aspectes dels llenguatges formals que es faran servir al llarg de tot el manual. A banda, en l’apèndix A s’ofereix una introducció als conceptes matemàtics més importants que es donaran per suposats.

1.1 Símbols, cadenes i llenguatges

Considerarem un conjunt finit i no buit de símbols que anomenarem alfabet o vocabulari. Per exemple {a, b, c} , {0,1,2,3,4,5,6,7, 8,9}o { 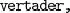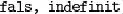} serien alfabets vàlids. El conjunt de tots els nombres enters 1no seria un alfabet vàlid.

Podem definir un símbolcom una etiqueta o una entitat que no té, en principi, cap significat i que és indivisible. Una cadena(de símbols), també anomenada moto paraula, és una successió finita de símbols d’un alfabet determinat.

Per exemple, aaabbba , 1024 i 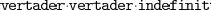2, serien exemples de cadenes sobre cada un dels alfabets anteriors.

Cada cadena de símbols té associada una longitud, que es defineix com el nombre de símbols que formen una cadena. Les cadenes anteriors tenen longitud 7, 4 i 3, respectivament. Escriurem la longitud d’una cadena x com a |x|.

Estendrem la notació per referirnos al nombre de símbols d’un cert tipus que conté una cadena. Així, si x és una cadena sobre ∑ i A és un subconjunt de ∑, |x| Arepresenta el nombre de símbols del conjunt A que conté x . Per al cas particular que A només continga un simbol, a, escriurem |x| aen lloc de |x| {a}. Per exemple, si x = aaabbba és una cadena sobre { a, b, c }, | x | a= 4, | x | b= 3, | x | c= 0, i | x |{ a, b} = | x | = 7.

Si anomenem P(∑) el conjunt de totes les possibles cadenes sobre un determinat alfabet 3, podem definir certes operacions internes dins d’aquest, la més important de les quals és la concatenacio.

Siguen x i y dues cadenes sobre un determinat alfabet £, anomenem concatenaciode x amb y la cadena resultant de juxtaposar les dues cadenes ( x a l’esquerra i y a la dreta), i la representem com x · y o simplement com a xy .

Es pot demostrar fàcilment que el conjunt P(∑) amb la operació • té estructura de monoidei, per tant, també de semigrup. L’element neutre d’aquest conjunt respecte de la concatenacio (que ho és per l’esquerra i per la dreta) és una cadena especial que no té cap símbol, anomenada cadena buidao cadena nul·la, i que escriurem en aquest manual 4com a ε.

Diem que una cadena y és prefixd’una altra cadena x si i només si existeix alguna cadena z tal que x = yz .

Diem que una cadena y és sufixd’una altra cadena x si i només si existeix alguna cadena z tal que x = zy .

Diem que una cadena y és factor(o infixo subcadena) d’una altra cadena x si i només si existeixen cadenes z i t tals que x = zyt .

Els prefixos i sufixos són casos particulars de factors. Es parla de factors (prefixos o sufixos) propis quan aquests són diferents de la cadena buida i de la cadena a que es refereixen.

Anomenem factoritzacióde x una descomposició de la cadena x en un nombre finit de factors, x = y1 · y1 ··· yk .

Siga un determinat alfabet ∑, anomenem llenguatge tot conjunt de cadenes sobre ∑.

Alguns exemples de llenguatges sobre els alfabets anteriors serien

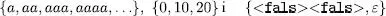
La talla o grandària d’un llenguatge, L, és la cardinalitat o nombre de cadenes corresponent, que escriurem com a |L| normalment. Les talles de cada un dels llenguatges que acabem de donar com a exemple serien ∞, 3 i 2, respectivament. Una forma més rigorosa d’expressar el primer d’aquests llenguatges és

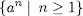
Sobre qualsevol alfabet, hi ha sempre dos llenguatges especials que reben el nom de llenguatge buiti llenguatge format per la cadena buidai que s’escriuen com a ∅ i {ε}, respectivament.

Aquests dos llenguatges són els elements neutres dins del conjunt de tots els possibles llenguatges respecte a les operacions uniói concatenació de llenguatges 5, respectivament.

Es pot demostrar que, respecte a aquestes dues operacions, el conjunt de tots els possibles llenguatges té estructura de monoide commutatiu o abelià i de monoide, respectivament.

Donat un alfabet ∑ qualsevol, s’hi suposa donada una relació d’ordre total que origina el que s’anomena ordenació alfabètica. A partir d’aquesta es pot definir una ordenació lexicogràficao ordenació canònicadel conjunt P(∑), que consisteix a ordenar-ne les cadenes de menor a major longitud i, dins d’una mateixa longitud, ordenar-les per ordre alfabètic 6.

Aquesta ordenació del conjunt P(∑) fa que es puga establir una correspondència biunívoca o bijecció entre aquest conjunt i els nombres naturals, la qual cosa implica que P(∑) és sempre un conjunt numerable.

1.1.1 Operacions amb cadenes

A banda de la concatenació, es poden definir altres operacions amb cadenes.

Es defineix la potència i -èsima d’una cadena x com la concatenació de x amb ella mateixa i vegades. S’escriu

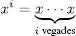
Es considera, per definició, que x0 = e.

La potència admet també una definició recursiva:

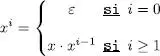
Compleix les propietats següents:

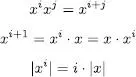
La inversió, reverso reflexiód’una cadena, que escriurem com a xR , és una altra cadena formada pels mateixos simbols però en ordre invers.