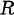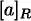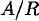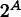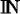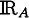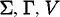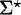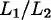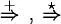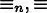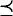Francesc Josep Ferri Rabasa - Teoria d'autòmats i llenguatges formals

Com reconeixen Hopcroft, Motwani i Ullman en la recent segona edició del seu famós llibre, les coses han canviat en els darrers vint anys i el que abans era una assignatura dels cursos més avançats i amb un caire marcadament matemàtic, ara se sol oferir en segon o tercer curs i amb la intenció (encertada) que són més importants els conceptes i les seues implicacions, que no el formalisme matemàtic emprat. Això no implica de cap manera que els conceptes s’hagen d’impartir (només) informalment. Precisament, en algunes titulacions d’informàtica, aquesta assignatura troncal és l’última gran assignatura teòrica i s’hauria de prendre com una oportunitat per potenciar el formalisme matemàtic i el pensar abans de fer entre els futurs informàtics .

L’organització és molt similar a altres llibres sobre autòmats i llenguatges. El capítol 1 conté una introducció general sobre el tipus d’enfocament que es presenta i introdueix les definicions relatives a símbols, cadenes i llenguatges. Aquest primer capítol i els tres següents es dediquen bàsicament a l’estudi dels llenguatges regulars, els autòmats finits i les expressions regulars, així com a les gramàtiques incontextuals i els seus corresponents acceptors. La major part d’aquests conceptes tenen aplicació directa a l’hora de construir compiladors, dissenyar llenguatges de programació o analitzar i processar cadenes de caràcters .

La resta de capítols, més que aplicacions, tenen conseqüències importantíssimes per entendre com i per què hi ha coses que no es poden calcular (capítols 5 i 6), i que hi ha càlculs que són possibles però no factibles (capítol 7). Al final s’ha inclòs una introducció a les funcions recursives en forma d’apèndix, juntament amb un altre apèndix sobre conceptes matemàtics .

Molts dels exemples i exercicis proposats provenen d’exàmens realitzats en els últims anys i s’ha intentat que cobresquen suficientment la totalitat de la matèria amb diversos graus de dificultat .

Aquest llibre ha estat planificat per ser utilitzat en una assignatura anual de 90 hores lectives i l’únic requisit són alguns coneixements bàsics d’àlgebra i matemàtica discreta .

En algunes universitats (com una alternativa també vàlida) es dóna clarament més pes a la primera part en detriment de la segona, almenys quant a troncalitat. Fins i tot en aquest cas, el present llibre pot fer-se també servir, ja que conté bàsicament tots els conceptes escaients i amb el rigor suficient. Tan sols caldria ampliar lleugerament el nombre d’exemples i problemes i potser ampliar el rigor i l’extensió de les demostracions d’alguns teoremes i les seues conseqüències quant a la primera part .

De ben diverses maneres aquest llibre ha rebut contribucions de moltes persones. De manera especial, i per proximitat acadèmica, de Salva Bayarri i d’Elena Díaz, així com d’Ariadna Fuertes. Alguns comentaris i discussions amb altres companys també han contribuït a donar forma i sentit a aquest llibre. Voldria anomenar Jesús Albert, Salva Moreno, Fernando Barber, Carlos Pérez, Juan Gutiérrez, Vicent Arnau, Gregorio Martín i, en general, tots els companys del Departament d’Informàtica de la Universitat de València. Finalment, voldria citar els companys Encarna Segarra i Pedro García de la Universitat Politècnica de València i també Rafa Carrasco i Mikel Forcada de la Universitat d’Alacant que han tingut l’amabilitat de llegir parts substancials del manuscrit i de comentar amb mi els seus punts de vista .

Burjassot, 25 de juny de 2004

SÍMBOLS UTILITZATS

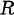	Relació binària d’equivalència.
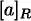	Classe d’equivalència de R que conté l’element a .
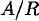	Conjunt quocient del conjunt A induït per la relació R .
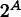	Conjunt potència de A o conjunt parts de A .
Ø	Conjunt buit, llenguatge buit.
ɛ	Cadena buida.
	Símbol blanc.
{ɛ}	Llenguatge format per la cadena buida.
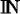	Nombres enters: 0, 1, 2,. ..
	Congruència associada a un llenguatge L .
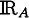	Congruència associada a un autòmat A .
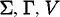	Alfabets o vocacularis.
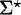	Monoide lliure sobre X.
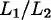	Quocient (per la dreta) del llenguatge L 1pel llenguatge L 2.
a, b, c,.. .	Símbols terminals (en gramàtiques).
X, Y, Z,.. .	Símbols no terminals.
x, y, z,.. .	Cadenes de símbols no terminals.
u, v, w,.. .	Cadenes de símbols terminals.
α, β,...	Cadenes de símbols de qualsevol tipus.
q •, P •	Tancament èpsilon d’un estat o d’un conjunt d’estats.
x R	Inversió o reflexió de la cadena x .
α → β	Producció.
	Derivació directa.
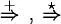	Tancament i tancament transitiu de =K
	Implicació lògica.
δ	Funció de transició.
	Moviment.
	Computació (tancament transitiu de 1—).
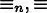	n-equivalència i equivalència entre estats.
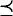	Reducció entre problemes.
	Reducció polinòmica entre problemes.
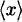	Codificació (efectiva) de x .

1. Llenguatges formals i computació