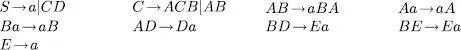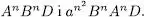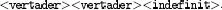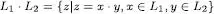1.4 Exercicis
Exercici 1.1Justifiqueu la regularitat del llenguatge 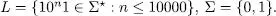
Exercici 1.2Demostreu que la classe dels llenguatges finits i la dels co-finits són disjuntes.
Exercici 1.3Siguen 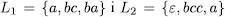 Calculeu els llenguatges
Calculeu els llenguatges 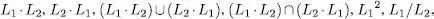
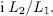
Exercici 1.4Trobeu una gramàtica (com més senzilla millor) que genere cadenes de zeros i uns que no tinguen dos símbols 1 consecutius. De quin tipus és el llenguatge generat?
Exercici 1.5Trobeu gramàtiques que generen els llenguatges 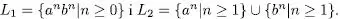
Exercici 1.6Escriviu una gramàtica que genere les cadenes de digits corresponents a nombres enters. Per exemple, 0, 1, 22, 2304 són correctes, però 0023 no.
Exercici 1.7Escriviu una gramàtica que genere les cadenes de dígits corresponents a nombres decimals. Per exemple, 0, 12.3, 0.15, 0.0000032.
Exercici 1.8Trobeu una gramàtica que genere cadenes en {0,1}*en les quals tot zero vaja necessàriament seguit d’un 1.
Exercici 1.9Trobeu una gramàtica que genere cadenes en en les quals hi haja el doble de zeros que d’uns.
Exercici 1.10Elimineu les regles nul·les en la gramàtica següent: 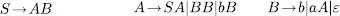
Exercici 1.11Calculeu el llenguatge generat per la gramàtica següent i trobeu una gramàtica equivalent tan senzilla com siga possible. De quin tipus és el llenguatge? 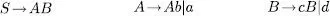
Exercici 1.12Justifiqueu que el llenguatge 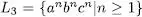 és generat per la gramàtica
és generat per la gramàtica 
Exercici 1.13Trobeu gramàtiques independents del context que generen els llenguatges següents:
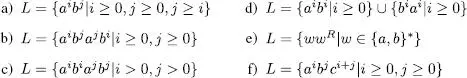
Exercici 1.14 Trobeu el llenguatge generat per la gramàtica següent i justifiqueu la resposta. 
Exercici 1.15 Digueu quin és el llenguatge generat per la gramàtica 
Exercici 1.16 Trobeu el llenguatge generat per la gramàtica

Exercici 1.17 Comproveu que el llenguatge 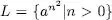 és generat per la gramàtica
és generat per la gramàtica
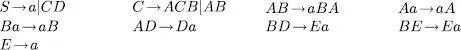
Suggeriment: considereu les formes sentencials 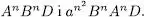
1No els nombres mateixos, sinó entesos com a símbols escrits en un paper, per exemple.
2Hem utilitzat el símbol per fer més clara la separació en símbols de la cadena. Una altra pràctica habitual en aquests casos és envoltar els símbols amb i. Aleshores escriuríem la cadena com a 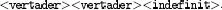
3Fem notar que aquest conjunt és infinit.
4En altres texts s’escriu també com a λ.
5L’operació concatenació s’estén trivialment al cas de llenguatges definint
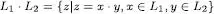
6Com es fa en els diccionaris.
7Recordem que, matemàticamente un homomorfisme (o morfisme) és tota aplicació f entre dos conjunts amb lleis de composició interna,( A , +) i ( B , ×), que compleix que f(x + y) = f(x) × f(y) per a tot parell d’elements de A . En aquest sentit també són homomorfismes les substitucions.
8Aquesta demostració de no numerabilitat es dóna al final de l’apèndix A.
9Hem decidit en aquest manual utilitzar la nomenclatura contextual i incontextual en lloc de la més correcta sensible al context i de context lliure . Així, doncs, cal tenir present que contextual o s’oposa a incontextual i és, per tant, diferent de no contextual.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

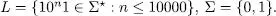
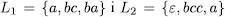 Calculeu els llenguatges
Calculeu els llenguatges 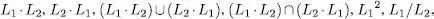
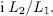
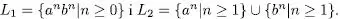
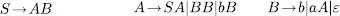
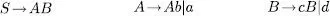
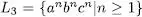 és generat per la gramàtica
és generat per la gramàtica 
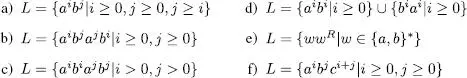



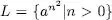 és generat per la gramàtica
és generat per la gramàtica