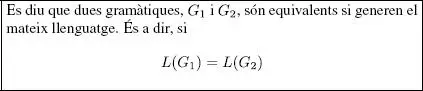
Es pot demostrar mitjançant un argument purament numèric i relativament senzill que hi ha llenguatges que no són generats per cap gramàtica. La demostració consisteix a mostrar que el conjunt de totes les gramàtiques sobre un determinat alfabet és numerable (atès que una gramàtica és una descripció finita), mentre que el conjunt de tots els possibles llenguatges sobre el mateix alfabet (igual que el conjunt potència de qualsevol conjunt infinit) és no numerable 8.
1.2.1 La jerarquia de Chomsky
Es pot distingir entre quatre tipus de gramàtiques d’acord amb la forma de les productions.
tipus 0o també gramàtiques estructurades per frases o gramàtiques sense restrictions . Les productions no tenen cap tipus de restricció additional.
tipus 1o també gramàtiques sensibles al context o gramàtiques contextuals .Les produccions han de ser necessàriament de la forma

on x i y són cadenes de V* , β és una cadena de V + i A és qualsevol símbol no terminal. El prefix x i el sufix y de la part esquerra (i dreta) de cada producció rep el nom de context.
tipus 2o també gramàtiques de context lliure, gramàtiques independents del context o gramàtiques incontextuals9 . Les produccions han de ser de la forma
A → a
on A és qualsevol símbol no terminal i a és qualsevol cadena de V*.
tipus 3o també gramàtiques regulars . Les produccions han de ser de la forma
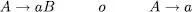
on A i B són símbols no terminals i a pot ser qualsevol cadena de terminals. Aquestes gramàtiques s’haurien d’anomenar propiament gramàtiques regulars per la dreta . Es poden definir de la mateixa manera les gramàtiques regulars per l’esquerra exigint que les produccions siguen de la forma A → Ba en comptes de A → aB com en la definició anterior. Es pot demostrar que ambdós tipus de gramàtiques són equivalents, en el sentit que per a tota gramàtica d’un tipus n’hi ha una de l’altre tipus que és equivalent. En aquest manual parlarem únicament de gramàtiques regulars i ens referirem sempre a les regulars per la dreta si no especifiquem el contrari.
Els quatre tipus de gramàtiques introduits indueixen quatre families de llenguatges segons el tipus de gramàtiques amb què es puguen generar.
Es diu que un llenguatge és de tipus N (N = 0,1,2,3) si hi ha alguna gramàtica de tipus N que el genere.
Com a conseqüència d’aquesta definició s’obtenen quatre classes de llenguatges incloses les unes dins de les altres com es mostra en la figura 1.1. Escriurem la classe formada pels llenguatges de tipus N com a N . Les classes de llenguatges de tipus 1, 2 i 3, les escriurem també com a  R, I i C , respectivament.
R, I i C , respectivament.
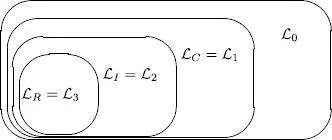
Figura 1.1: Relació entre les diferents classes de llenguatges induïdes per la jerarquia de Chomsky.
Donada una classe de llenguatges qualsevol, 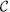 , es defineix la classe co
, es defineix la classe co 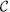 com a
com a
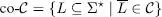
Per exemple, la classe dels llenguatges co-regulars, o co-R , està formada per llenguatges els complementaris dels quals són regulars.
Un altre parell de classes que són interessants (ser la seua simplicitat) són els llenguatges finits i els co-finits. Es pot demostrar molt fàcilment (i es deixa com a exercici) que tot llenguatge finit és regular.
1.2.2 Transformació de gramàtiques
Les produccions de les gramàtiques es poden manipular de diverses maneres, de forma que el llenguatge generat no canvia. En el cas particular de les gramàtiques incontextuals hi ha algunes operacions especialment interessants.
Substitució o desplegament
Siga A un símbol no terminal d’una gramàtica incontextual ∈ i siga
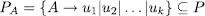
el conjunt de produccions que tenen A com a part esquerra.
Donada una producció de G de la forma X → αAß amb X ≠ A , es pot substituir per
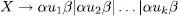
La gramàtica resultant és equivalent, ja que cada una d’aquestes noves produccions representa l’efecte de dues produccions originals. Remarquem el fet que les produccions de Pa segueixen estant en la nova gramàtica i que només X —y αAß ha desaparegut.
Aquesta transformació es pot fer servir per eliminar les anomenades regles de redenominació de la forma A → B . Per exemple, la gramàtica
S → AB\Aa\bA
A → Aab\Aba\ε
B → bB\b\A
és equivalent a
S → AB\Aa\bA
A → Aab\Aba\ε
B → bB\b\Aab\Aba\ε
Factorització
Siga un conjunt de produccions de la forma
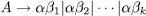
de manera que totes les parts esquerres coincideixen i les parts dretes comparteixen un determinat prefix a. Aquestes produccions es poden, doncs, substituir per
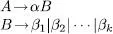
on B és un nou símbol no terminal.
Eliminació d’una producció
Siga  una producció no recursiva i
una producció no recursiva i 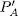 ⊆ P el conjunt de produccions en les quals A apareix en la part dreta. Aleshores, la producció
⊆ P el conjunt de produccions en les quals A apareix en la part dreta. Aleshores, la producció  es pot eliminar si per cada producció de
es pot eliminar si per cada producció de 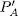 de la forma X → αAß se n’afegeix una altra X → αγß .
de la forma X → αAß se n’afegeix una altra X → αγß .
Читать дальше

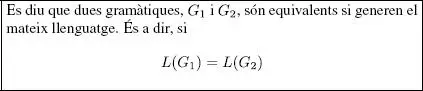

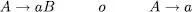
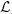 R, I i C , respectivament.
R, I i C , respectivament.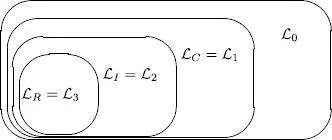
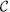 , es defineix la classe co
, es defineix la classe co 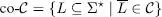
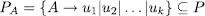
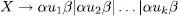
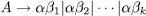
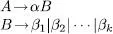
 una producció no recursiva i
una producció no recursiva i 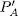 ⊆ P el conjunt de produccions en les quals A apareix en la part dreta. Aleshores, la producció
⊆ P el conjunt de produccions en les quals A apareix en la part dreta. Aleshores, la producció 










