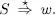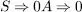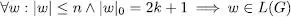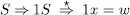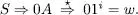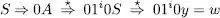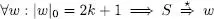La gramàtica resultant és equivalent, ja que les noves produccions reprodueixen l’efecte de les originals (que no desapareixen) juntament amb el de la producció  .
.
Un cas particular d’aquest és l’eliminació de regles nul·les de la forma A → ε amb A ≠ S.
Per exemple, donada la gramàtica
S → abA\baB\a
A → bB\abA\ε
B → aA\baB\ε
es pot convertir en la gramàtica següent eliminant les dues regles nul·les.
S → abA\baB\ab\ba\a
A → bB\abA\b\ab
B → aA\baB\a\ba
Modificació de bucles
Un buclesimple en una gramàtica incontextual consisteix en dos conjunts de produccions associades a un mateix símbol. En el primer conjunt apareix aquest símbol i en el segon conjunt no. Si aquest símbol apareix en la part dreta en la posició més a l’esquerra es parla de bucle a esquerres o recursivitat a esquerres.
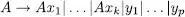
i si apareix en la posició més a la dreta es parla de bucle a dretes o recursivitat a dretes.
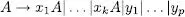
Sempre es pot substituir un tipus de recursivitat per l’altre sense que el llenguatge es modifique. Per exemple, la recursivitat a dretes anterior es pot substituir per les produccions següents:
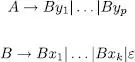
La conversió en sentit contrari es faria igualment.
1.2.3 Verificació de gramàtiques
Les gramàtiques consitueixen una eina fonamental per a descriure de manera compacta i clara llenguatges que són intrínsecament complexos. No obstant això, de vegades pot resultar complicat establir l’equivalència entre el llenguatge generat per una gramàtica i el llenguatge expressat mitjançant algun altre formalisme. El fet de demostrar rigorosament l’equivalència entre un llenguatge descrit formalment i una gramàtica s’anomena verificar la gramàtica.
Aquesta verificació requereix normalment algun tipus de demostració per inducció donada la natura recursiva de les gramàtiques. En aquest manual, no verificarem normalment les gramàtiques, ja que l’equivalència entre aquestes i els corresponents llenguatges estarà suficientment clara.
Exemple 1.1 Demostrar que el llenguatge L format per les cadenes w ϵ {0,1}* que compleixen |w| 0= 2 k + 1 per a algun enter k, és generat per la gramàtica ∈ donada per
S → 1S|0A
A → L4|0S| ε
Primer cal demostrar que L(G) C L , per a la qual cosa cal caracteritzar les cadenes que genera G.
Per inspecció de les produccions associades a S és evident que
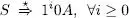
Pel mateix motiu, les produccions associades a a porten a
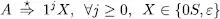
Combinant els dos resultats anteriors
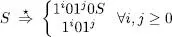
Per tant, es pot afirmar que
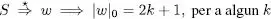
d’on es conclou que L(G) ⊆ L .
En segon lloc, cal demostrar també que L ⊆ L(G). És a dir, que 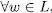 ,
, 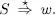
Ho demostrarem per inducció en la talla de w .
B.I.L’única cadena de L de talla menor o igual que 1 és 0, i es compleix
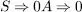
H.I. 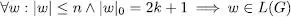
P.I. Siga w amb | w | = n i | w | 0= 2k + 1. Hi haurà dos casos:
1. w = lx i aleshores x compleix la hipótesi d’inducció i per tant
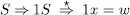
2. w = 0x. x tindrà un nombre parell de zeros i hi haurà dos subcasos:
(a) x = 1 ies té que 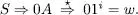
(b) x = 1 i0 y on y ha de contenir necessàriament 2 l + 1 zeros i compleix la hipótesi d’inducció. Aleshores,
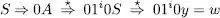
En els dos casos es pot trobar una derivació i aleshores es pot concloure
que
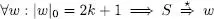
i per tant L ⊆ L(G) .
1.3 Acceptació de llenguatges i computabilitat
De la mateixa manera que s’ha estudiat l’aspecte generatiu dels llenguatges es pot plantejar el problema contrari. És a dir, donada una cadena x qualsevol i una descripció (finita) d’un llenguatge, pertany la cadena x a aquest llenguatge?
Aquesta pregunta es pot plantejar per a descriptions de llenguatges mijantçant gramàtiques, però el problema no és gens trivial fins i tot per a llenguatges relativament senzills.
Per aquesta raó és convenient definir el que s’anomenen acceptorso autòmats, que es poden veure com a dispositius lògics que processen cadenes i decideixen sobre aquestes (les accepten o no). Això no és més que una altra forma de descriure llenguatges. Donat qualsevol autòmat no trivial, es pot definir el llenguatge associat a l’autòmat com aquell que està format per les cadenes que l’autòmat accepta.
Definirem al llarg d’aquest manual una família d’autòmats, el més general dels quals és el que es coneix com a màquina de Turing. Veurem que hi ha relacions estretes entre els diferents tipus d’autòmats i les gramàtiques de la jerarquia de Chomsky. A més a més, s’estudiarà la relació entre el tipus de processament que pot fer l’autòmat més general i els límits del que es pot o no es pot computar des del punt de vista d’obtenció de solucions algorísmiques a problemes.
Читать дальше

 .
.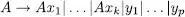
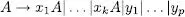
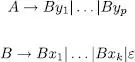
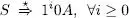
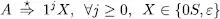
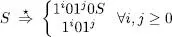
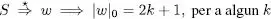
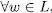 ,
,