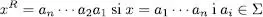
La inversió també admet la definició recursiva següent:
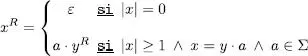
1.1.2 Operations amb llenguatges
Com que els llenguatges són conjunts (de cadenes), s’hi poden aplicar totes les operacions usuals sobre conjunts, com ara la unió, la intersecció, el complement i la resta. Aquestes operacions, les escriurem com a

A més a més, les operacions amb cadenes es poden estendre al cas de llenguatges, de la mateixa manera que s’ha fet amb la concatenació.
En general, donada qualsevol operació interna m-ària amb cadenes, O, la seua extensió a llenguatges és donada per
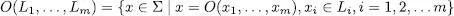
A banda, hi ha altres operacions especifiques amb llenguatges.
El quocient de dos llenguatges, L 1i L 2, és donat pels prefixos d’aquelles cadenes de L 1que es poden factoritzar com el mateix prefix seguit d’un sufix en L 2.
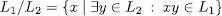
L’operació quocient també es pot definir per a cadenes:

Per exemple, abc/c = ab i abc/ac no està definit.
Aquesta operació també s’anomena quocient per la dretai es pot veure com la inversa de la operació concatenació per la dreta.
La extensió a llenguatges es pot dur a terme com a quocient entre un llenguatge i una cadena
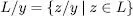
i també com a quocient entre dos llenguatges
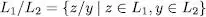
Aquesta darrera definició és equivalent a la primera que s’ha donat.
Per exemple, si L1 = {a n | n ≥ 0 i L 2 = {an bm | n, m ≥ 0}, aleshores L 1/a = L 1, L 2/ /b = L 2i L 2/ /a = L1 .
De la mateixa manera es poden definir també els quocients per l’esquerra entre cadenes o llenguatges. En alguns textos els quocients entre z i y per la dreta i per l’esquerra s’escriuen com a zy –1i y –1 z , respectivament.
El quocient per l’esquerra entre una cadena x i un llenguatge L , x –1L, s’anomena derivadade L respecte de xi està format pels anomenats sufixos de x en L (també de vegades bons finalsde x en L ).
Per exemple, 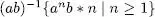 està format per cadenes de zero o més símbols b perqué són les úniques que afegides a ab estàn en
està format per cadenes de zero o més símbols b perqué són les úniques que afegides a ab estàn en 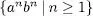
Anomenem substitucióuna funció que a cada símbol d’un alfabet ∑ li fa correspondre un llenguatge sobre un altre alfabet 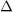 .
.
Matemàticament,

La substitució s’estén trivialment a cadenes. Donada una cadena, la substitució que s’hi aplique donarà com a resultat la concatenació de les substitucions sobre cada un dels seus símbols.
Perquè tinga sentit, cal definir la substitució sobre la cadena buida, que ha de donar lògicament la cadena buida.
Escrivint-ho recursivament:
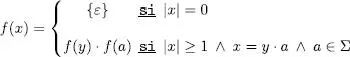
També ho podem escriure com
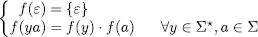
Les substitucions s’estenen també trivialment per a llenguatges de la manera següent:
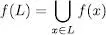
Un cas particular de substitució és l’ homomorfisme 7que és una substitució en la qual es compleix que a tot símbol de ∑ li correspon (com a màxim) una única cadena de  . És a dir, h : *. Normalment escriurem les substitucions com a f i els homomorfismes com a h .
. És a dir, h : *. Normalment escriurem les substitucions com a f i els homomorfismes com a h .
Considerem com a exemple una substitució entre els alfabets {0,1} i {a, b, c} donada per
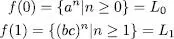
Aleshores es compliria que
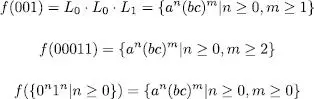
Donat un homomorfisme h :  , anomenem homomorfisme inversde la cadena y ∈
, anomenem homomorfisme inversde la cadena y ∈  , i ho escrivim com a h –1( y ), el conjunt de cadenes de ∑* tals que transformades per h donen y . És a dir,
, i ho escrivim com a h –1( y ), el conjunt de cadenes de ∑* tals que transformades per h donen y . És a dir,
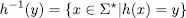
També es pot definir l’homomorfisme invers d’un llenguatge quasi de la mateixa manera.
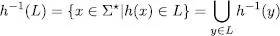
Considerem com a exemple el llenguatge 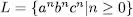 i l’homomorfisme donat per h(0) = ab, h (1) = b, h (2) = a, h (3) = cc . Aleshores es compleix que
i l’homomorfisme donat per h(0) = ab, h (1) = b, h (2) = a, h (3) = cc . Aleshores es compleix que
Читать дальше

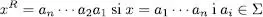
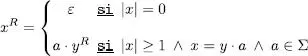

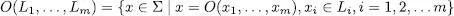
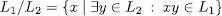

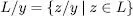
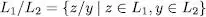
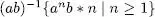 està format per cadenes de zero o més símbols b perqué són les úniques que afegides a ab estàn en
està format per cadenes de zero o més símbols b perqué són les úniques que afegides a ab estàn en 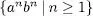
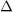 .
.
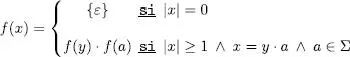
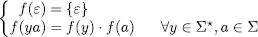
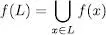
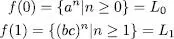
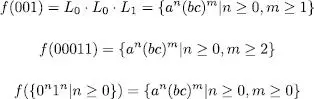
 , anomenem homomorfisme inversde la cadena y ∈
, anomenem homomorfisme inversde la cadena y ∈ 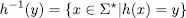
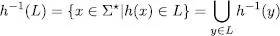
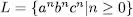 i l’homomorfisme donat per h(0) = ab, h (1) = b, h (2) = a, h (3) = cc . Aleshores es compleix que
i l’homomorfisme donat per h(0) = ab, h (1) = b, h (2) = a, h (3) = cc . Aleshores es compleix que










