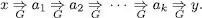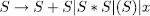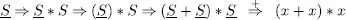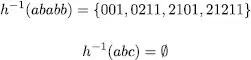
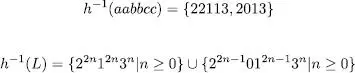
Per a tot homomorfisme sempre es compleix que
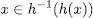
i també
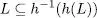
Per a l’exemple anterior es té que
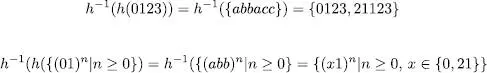
És important adonar-se que la propietat anterior no es compleix si intercanviem l’ordre d’aplicacio de l’homomorfisme i l’invers. Seguint amb el mateix exemple, tenim que
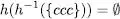

Si de l’anterior definició s’exclou el terme L0 , s’obté l’anomenat tancament positiu:
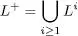
Si, abusant de la notació, considerem l’alfabet E com un llenguatge finit format per cadenes de longitud 1, podem escriure

Aquests dos conjunts reben el nom de monoide lliurei semigrup lliureengendrats per E. D’ara endavant utilitzarem aquests noms i la notació ∑* i ∑ +per referirnos a aquests conjunts.
En el context de la teoria de llenguatges formals només tenen importància els llenguatges que són infinits. Fins i tot dins d’aquests, els més importants són els que defineixen les cadenes que hi pertanyen en funció d’una certa estructura dins de les cadenes.
1.2 Generació de llenguatges
En el context de la teoria de llenguatges formals només tenen importància els llenguatges que són infinits. Fins i tot dins d’aquests, els més importants són els que defineixen les cadenes que i ertanyen en funció d’una certa estructura dins de les cadenes.
Un exemple d’aquest tipus de llenguatge és el que està format per aquelles cadenes sobre l’alfabet ∑ ex= {x, +, *, (, )} que són expressions aritmètiques vàlides (ben parentitzades). És a dir,

Encara que és ben clar quin és aquest llenguatge, no pot ser definit d’una forma compacta (amb una descripció finita) de la mateixa manera que s’ha fet en els exemples anteriors.
Una forma de definir aquest tipus de llenguatges és mitjançant una definició recursiva. Un mecanisme que permet introduir definicions recursives en el context de cadenes de símbols és donat pels sistemes de reescriptura, un cas particular dels quals són les gramàtiques.

Els elements de l’alfabet no terminal, VN , s’anomenen símbols no terminals, símbols auxiliarso, simplement, variablesde la gramàtica.
Una producció α → ß significa que la cadena a es pot reescriure com a ß (es pot canviar l’una per l’altra). Ens referirem a α i a β com les parts esquerra i dreta de la producció, respectivament. Per representar de forma compacta diverses produccions amb la mateixa part esquerra escriurem
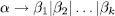
en lloc de
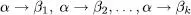
Diem que una cadena y deriva directament d’una cadena x segons una gramàtica G, i ho escrivim com a 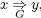 si i només si
si i només si 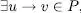 , de forma que
, de forma que 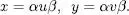
Diem que una cadena y deriva d’una cadena x segons una gramàtica, i ho escrivim com a 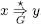 si i només si x = y o si existeix una seqüència finita de paraules
si i només si x = y o si existeix una seqüència finita de paraules 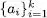 tal que
tal que 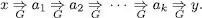
Si, pel context, està clar a quina gramàtica ens estem referint, suprimirem la referència a la gramàtica ∈ en el símbol ⇒.
Les cadenes de Vque es poden derivar a partir de l’axioma reben el nom de formes sentencialsde G . Si, a més a mes, són cadenes exclusivament de Vt es diu que són sentènciesde G .

Per exemple, el llenguatge L exés generat per la gramàtica

on P és
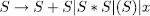
Un exemple de derivació amb aquesta gramàtica seria
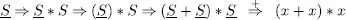
En aquest exemple hem subratllat en cada forma sentencial els símbols no terminals sobre els quals s’aplica la producció següent (la producció que s’aplica és òbvia per inspecció de la cadena derivada).
Читать дальше

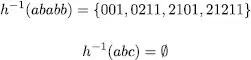
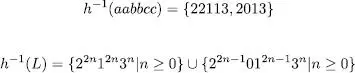
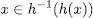
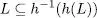
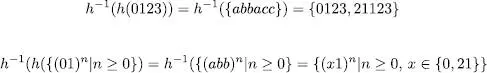
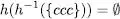

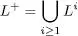



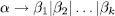
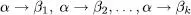
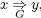 si i només si
si i només si 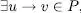 , de forma que
, de forma que 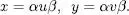
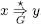 si i només si x = y o si existeix una seqüència finita de paraules
si i només si x = y o si existeix una seqüència finita de paraules 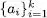 tal que
tal que