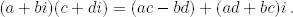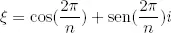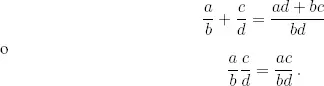
Es sencillo construir el conjunto de los números racionales a partir de los números enteros como clases de equivalencia . (En el problema 1.10, explicamos cómo hacer esta construcción).
En la segunda parte de este libro, cuando desarrollemos la teoría de Galois, trabajaremos con el conjunto de números reales ℝ y el de los complejos ℂ. La construcción rigurosa de ℝ es uno de los hitos de la matemática del siglo XIX, pero esta es materia de nuestros colegas los analistas. Apenas utilizaremos propiedades de los números reales, más que aquellas que están directamente asociadas a su suma, multiplicación (ℝ es un cuerpo ) y a los polinomios. Por ejemplo, dado 0 ≤ a ∈ ℝ y 0 < n ∈ ℕ supondremos que existe un único número real 0 ≤ b ∈ ℝ tal que b n = a . Este número b se escribe 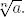 Un número real a ∈ ℝ es irracionalsi a ∉ ℚ. Como los ceros del polinomio x n− 1 son fundamentales en teoría de Galois, un poco de trigonometría también será necesaria.
Un número real a ∈ ℝ es irracionalsi a ∉ ℚ. Como los ceros del polinomio x n− 1 son fundamentales en teoría de Galois, un poco de trigonometría también será necesaria.
Recordamos que un entero n ∈ ℕ es un cuadradosi n = a 2para cierto a ∈ N.
Teorema 1.16 Sean n , m ∈ ℕ no cero con mcd( n , m ) = 1. Entonces 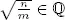 si y solo si n y m son cuadrados .
si y solo si n y m son cuadrados .
Demostración.Suponemos que 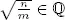 , y probamos que n y m son cuadrados. Por ejemplo, probamos que n es un cuadrado. Sea p un primo y supongamos que p f es la mayor potencia de p que divide a n con f ≥ 1. Es suficiente con probar que f es par y luego utilizar el teorema fundamental de la aritmética. Por hipótesis, podemos escribir
, y probamos que n y m son cuadrados. Por ejemplo, probamos que n es un cuadrado. Sea p un primo y supongamos que p f es la mayor potencia de p que divide a n con f ≥ 1. Es suficiente con probar que f es par y luego utilizar el teorema fundamental de la aritmética. Por hipótesis, podemos escribir
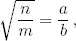
donde a , b ∈ ℕ. Entonces
b 2 n = a 2 m .
Como n y m son coprimos, sabemos que p no divide a m . Por tanto, si p e es la mayor potencia de p que divide a b , tenemos que 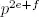 es la mayor potencia de p que divide a a 2. Concluimos que 2 e + f es par, y por tanto, también lo es f . Por el teorema fundamental de la aritmética, concluimos que n es un cuadrado. La implicación contraria es trivial.
es la mayor potencia de p que divide a a 2. Concluimos que 2 e + f es par, y por tanto, también lo es f . Por el teorema fundamental de la aritmética, concluimos que n es un cuadrado. La implicación contraria es trivial. 
Como decimos, en la segunda parte del libro estaremos interesados en polinomios y en sus ráıces. Por ejemplo, ¿cuáles son los ceros del polinomio x 8− 1? Para contestar, necesitamos trabajar con números complejos y una cierta trigonometría.
El cuerpo de los nú meros complejosℂ se define formalmente como el conjunto ℝ 2= {( a , b ) | a , b ∈ ℝ} con la suma ( a , b ) + ( c , d ) = ( a + c , b + d ) y la multiplicación ( a , b )( c , d ) = ( ac−bd , ad + bc ). Si llamamos i = (0, 1), vemos que i 2= (−1, 0). Si identificamos a con ( a , 0), podemos escribir ( a , b ) = a + bi , que es la notación que vamos a utilizar. Así, por ejemplo, tenemos que ℝ ⊆ ℂ o que
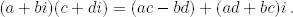
Teorema 1.17 (fórmula de De Moivre) Si a ∈ ℝ y n ∈ ℕ, entonces
(cos( a ) + sen( a ) i ) n = cos( na ) + sen( na ) i .
Demostración.Si suponemos las igualdades trigonométricas
cos( α + β ) = cos( α )cos( β ) − sen( α )sen( β )
y
sen( α + β ) = sen( α )cos( β ) + cos( α )sen( β ),
la fórmula de De Moivre es inmediata por inducción sobre n . 
Con la fórmula de De Moivre, ya podemos calcular los ceros del polinomio x n− 1: son los n números complejos ξ k , donde
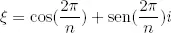
y 0 ≤ k ≤ n− 1. Estos n números complejos son muy importantes y se denominan las ráıces n -ésimas de la unidad. Los podemos situar en la circunferencia de radio 1 al dividirla en n -ángulos iguales. Por ejemplo, las ráıces 4-ésimas de la unidad son {1, i , −1, −i }.
PROBLEMAS
1.Sean A , B , C conjuntos. Probar:
(i) Si A ∩ B = A ∩ C y A ∪ B = A ∪ C , entonces B = C .
(ii) ( A − B ) ∪ ( B − A ) = ( A ∪ B ) − ( A ∩ B ).
(iii) A ∩ ( B − C ) = ( A ∩ B ) − ( A ∩ C ).
(iv) A − ( A − B ) = A ∩ B .
(v) ( B ∪ C ) − A = ( B − A ) ∪ ( C − A ).
(vi) ( A − B ) − C = ( A − B ) ∩ ( A − C ).
2.Sea f : X → Y una aplicación. Si A ⊆ X , se define f ( A ) = { f ( a ) | a ∈ A }. Si B ⊆ Y , se define f −1( B ) = { x ∈ X | f ( x ) ∈ B }.
(i) Si A ⊆ X , probar que A ⊆ f − 1( f ( A )).
(ii) Probar que f es injectiva si y solo si A = f − 1( f ( A )) para todo A ⊆ X .
(iii) Si B ⊆ Y , probar que f ( f − 1( B )) ⊆ B .
(iv) Probar que f es suprayectiva si y solo si f ( f − 1( B )) = B para todo B ⊆ Y .
3.Sea f : X → Y una aplicación. Si A y B son subconjuntos de X , probar que f ( A ∪ B ) = f ( A ) ∪ f ( B ) y f ( A ∩ B ) ⊆ f ( A ) ∩ f ( B ). Probar que f ( A ∩ B ) = f ( A ) ∩ f ( B ) para todos los subconjuntos A , B ⊆ X si y solo si f es inyectiva.
Читать дальше

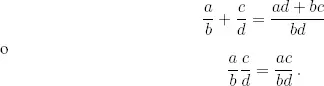
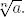 Un número real a ∈ ℝ es irracionalsi a ∉ ℚ. Como los ceros del polinomio x n− 1 son fundamentales en teoría de Galois, un poco de trigonometría también será necesaria.
Un número real a ∈ ℝ es irracionalsi a ∉ ℚ. Como los ceros del polinomio x n− 1 son fundamentales en teoría de Galois, un poco de trigonometría también será necesaria. si y solo si n y m son cuadrados .
si y solo si n y m son cuadrados .
 es la mayor potencia de p que divide a a 2. Concluimos que 2 e + f es par, y por tanto, también lo es f . Por el teorema fundamental de la aritmética, concluimos que n es un cuadrado. La implicación contraria es trivial.
es la mayor potencia de p que divide a a 2. Concluimos que 2 e + f es par, y por tanto, también lo es f . Por el teorema fundamental de la aritmética, concluimos que n es un cuadrado. La implicación contraria es trivial.