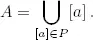Gabriel Navarro Ortega - Un curso de álgebra

Si A es un conjunto con una relación de equivalencia R , para cada a ∈ A se define [ a ] = { b ∈ A | ( a , b ) ∈ R }, que se llama la clase de equivalencia de a . Observamos que a ∈ [ a ] ⊆ A .

Teorema 1.6 Sea A un conjunto con R una relación de equivalencia , y sea P = {[ a ] | a ∈ A } el conjunto de clases de equivalencia de A. Entonces P es una partición de A .

Demostración.Como a ∈ [ a ], está claro que [ a ] ≠ ∅ y que

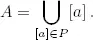
Si c ∈ [ a ], probamos a continuación que [ c ] = [ a ]. Sea x ∈ [ c ]. Entonces ( x , c ) ∈ R . Como ( c , a ) ∈ R , tenemos que ( x , a ) ∈ R y x ∈ [ a ]. Recíprocamente, si x ∈ [ a ], entonces ( x , a ) ∈ R . Como ( a , c ) ∈ R , tenemos que ( x , c ) ∈ R y x ∈ [ c ], como queríamos. Finalmente, supongamos que [ a ] ∩ [ b ] ≠ ∅, y sea c ∈ [ a ] ∩ [ b ]. Por lo anterior, tenemos que [ a ] = [ c ] = [ b ].

4

¿Todos los conjuntos infinitos tienen el mismo número de elementos? ¿Hay algún conjunto infinito con menos elementos que ℕ? ¿Cómo comparamos infinitos?

Al principio, puede que la intuición no nos sea del todo útil. Es famoso el Hotel de Hilbert que tiene un número infinito de habitaciones numeradas {1, 2, 3, …}, todas ellas ocupadas.

Al llegar un huésped nuevo, el conserje del hotel, lejos de rechazarlo, traslada al ocupante de la habitación n a la n +1, y deja así la primera habitación libre para el huésped nuevo. Este conserje ni se inmuta cuando momentos después ve aparecer llegando a su hotel un autobús con infinitos turistas {1, 2, 3, …}: traslada al ocupante de la habitación n a la habitación 2 n y al turista m a la habitación 2 m − 1. Tampoco se preocupa el conserje cuando esta vez aparece un número infinito de autobuses { a 1, a 2, …, a k , …} cada uno de ellos cargado de infinitos turistas { a k 1, a k 2, …}… pero vamos a dejarlo aquí.

Para comparar infinitos, las funciones biyectivas son fundamentales. Si existe f : A → B biyectiva, decimos que A y B tienen el mismo cardinal(o son equipotentes), y lo escribimos | A | = | B |. En caso contrario, escribimos | A | ≠ | B |.

Teorema 1.7 Sean A , B y C conjuntos .

(a) | A | = | A |.

(b) Si | A | = | B |, entonces | B | = | A |.

(c) Si | A | = | B | y | B | = | C |, entonces | A | = | C |.

Demostración.Para probar (a), utilizamos la función identidad 1 A. Si existe una función biyectiva f : A → B , entonces f − 1es biyectiva, y (b) queda probado. Para probar (c), usamos que la composición de funciones biyectivas es biyectiva por el lema 1.3.

El lector debe ser consciente de que en el teorema anterior, no hemos escrito que tener el mismo cardinal establece una relación de equivalencia pues a continuación estaríamos obligados a añadir “en el conjunto de todos los conjuntos”, y como ya hemos dicho antes, no debemos tratar con conjuntos demasiado grandes . Al principio de este capítulo, habíamos definido | A | para un conjunto finito A , como el número de elementos de A . Los ejercicios 1.2 y 1.3 nos aseguran que la notación | A | = | B | es consistente.

Asociado a un conjunto A hay otro conjunto especial que hemos utilizado en el ejemplo 1.2 (e):

P ( A ) = { B | B ⊆ A }

que se llama el conjunto potenciade A (o partesde A ). Lo más importante de P ( A ) es que tiene más elementos que A .

Teorema 1.8 Sea A un conjunto .

(a) La aplicación f : A → P ( A ) dada por f ( a ) = { a } es inyectiva .

(b) No existe ninguna aplicación g : A → P ( A ) suprayectiva .

Demostración.La primera parte es trivial. Sea ahora g : A → P ( A ) suprayectiva. Sea B = { a ∈ A | a ∉ g ( a )} ⊆ A . Como g es suprayectiva, entonces existe a ∈ A tal que g ( a ) = B . Si a ∈ B , entonces a ∉ g ( a ) = B , lo cual no es posible. Si a ∉ B , entonces a ∈ g ( a ), y por tanto a ∈ B , lo cual tampoco es posible.

Según el teorema 1.8, P (ℕ) tiene más elementos que ℕ, y de hecho se puede probar que | P (ℕ)| = |ℝ|. No nos podemos resistir a mencionar la llamada hipótesis del continuo , establecida por George Cantor en 1878. Si A y B son conjuntos, escribimos | A | ≤ | B | si existe f : A → B inyectiva, y | A | < | B | si | A | ≤ | B | y | A | ≠ | B |. Por ejemplo, acabamos de probar que | A | < | P ( A )| para todo conjunto A . La hipótesis del continuo, que constituye el primer problema de la famosa lista de problemas propuestos por Hilbert, afirma que no existe ningún conjunto A tal que |ℕ| < | A | < |ℝ|. En 1963 Paul Cohen probó que este enunciado es indemostrable . Este es otro concepto que no cabe en el presente libro. El autor sinceramente espera no haber interesado demasiado al lector en lógica para que renuncie al álgebra.

La siguiente propiedad de ℕ es fundamental: nos dice que en ℕ existe un buen orden .

Teorema 1.9 (teorema del buen orden enℕ ) Si A es un subconjunto no vacío de ℕ entonces existe a ∈ A tal que a ≤ b para todo b ∈ A. Este elemento a es único .

Demostración.Primero probamos la existencia de a . Como A no es vacío, sea a 1∈ A . Si a 1≤ b para todo b ∈ A , ya tendríamos el elemento que buscamos. En caso contrario, existe a 2∈ A tal que a 2 < a 1. Si a 2≤ b para todo b ∈ A , de nuevo lo tendríamos. Como entre 0 y a 1hay solo un número finito de elementos, este proceso no se puede repetir un número infinito de veces. Así, podemos llegar a encontrar a ∈ A tal que a ≤ b para todo b ∈ A .