Dados dos conjuntos A y B , podemos construir nuevos conjuntos. Por ejemplo, la uniónde A y B es el conjunto
A ∪ B = { x | x ∈ A ó x ∈ B }.
La intersecciónes el conjunto
A ∩ B = { x | x ∈ A y x ∈ B }.
La diferenciade A y B es
A − B = { x | x ∈ A y x ∉ B }.
El producto cartesianode A y B es el conjunto de pares
A × B = {( a, b ) | a ∈ A , b ∈ B },
donde entendemos que ( a , b ) = ( a′ , b′ ) si y solo si a = a′ y b = b′ .
Si A = {1, 2, 3} y B = {3, 4}, entonces A ∪ B = {1, 2, 3, 4}, A ∩ B = {3}, A − B = {1, 2} y A × B = {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}.
Desde luego, podemos unir o intersectar una colección arbitraria de conjuntos. Si I es un conjunto, y para cada i ∈ I tenemos definido un conjunto A i , que depende de i , entonces definimos

Por ejemplo, si para n ∈ ℕ, definimos A n = { m ∈ ℕ | m ≥ n }, entonces tenemos que
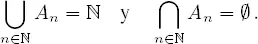
Si A 1, …, A n son conjuntos, definimos
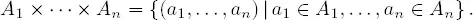
Si el lector está leyendo este primer capítulo, cabe la posibilidad de que no esté demasiado habituado a probar teoremas, habilidad que solo se adquiere con práctica, y leyendo muchas demostraciones. Probamos nuestro primer teorema.
Teorema 1.1 (Leyes de Morgan) Supongamos que X , I y A ipara i ∈ I son conjuntos. Entonces
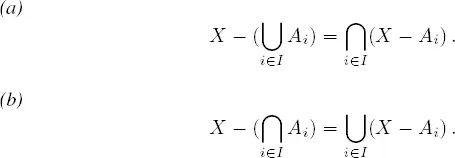
Demostración.Probamos (a), por ejemplo. Queremos probar que dos conjuntos son iguales. Por tanto, debemos probar que X − (⋃ i∈I A i ) está contenido en ⋂ i∈I( X − A i ), y la inclusión contraria. Sea x ∈ X − (⋃ i∈I A i ). Esto significa que x ∈ X y que x ∉ ⋃ i∈I A i . Por la definición de unión de una colección de conjuntos, tenemos que x ∉ A i para todo i ∈ I . Así, x ∈ X − A i para todo i ∈ I , y por la definición de intersección de una colección de conjuntos, concluimos que x ∈ ⋂ i∈I( X − A i ). Recíprocamente, si x ∈ ⋂ i∈I( X − A i ), tenemos que x ∈ X y x ∉ A i para todo i . Entonces x ∈ X y x ∉ ⋃ i∈I A i , y por tanto x ∈ X − (⋃ i∈I A i ). 
2
Los conjuntos se relacionan mediante aplicaciones . Si A y B son conjuntos, una aplicacióno función de A en B , que escribimos
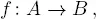
es una correspondencia (regla o criterio) que asigna a cada elemento a ∈ A un único elemento f ( a ) de B . A f ( a ) se le llama la imagende a mediante f . El conjunto A se llama el dominioo conjunto inicialde f . El conjunto B se llama el codominioo conjunto finalde f . El conjunto imagen
f ( A ) = { f ( a ) | a ∈ A }
es el subconjunto de B formado por todas las imágenes mediante f de los elementos de A .
Podemos imaginar una función como una máquina cuyos inputs son los elementos de A . Damos a ∈ A a la máquina y esta produce un output perfectamente determinado que es f ( a ) ∈ B . Para el lector riguroso que no esté satisfecho ni con la definición ni con la idea de la máquina , podemos definir una función f : A → B como un subconjunto X ⊆ A × B tal que X ∩ ({ a } × B ) tiene exactamente un elemento para todo a ∈ A ; pero esto es innecesariamente complicado. Si pensamos un momento sobre esta última definición, observamos que X es el grafo de la función f .
El lector está seguramente acostumbrado a tratar con funciones entre números reales como las aplicaciones f : ℝ → ℝ dada por f ( x ) = x 2+ 1, o g : ℝ → ℝ dada por g ( x ) = sen( x ). O incluso con funciones h : ℝ × ℝ → ℝ definidas por 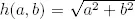 . (En estos ejemplos tendríamos que f (ℝ) = { a ∈ ℝ | a ≥ 1}, g (ℝ) = [−1, 1] y h (ℝ × ℝ) = { a ∈ ℝ | a ≥ 0}). Pero quizá el lector está menos acostumbrado a tratar con funciones sobre otros conjuntos, especialmente finitos. Por ejemplo, si A = {1, 2} y B = {2, 3} hay exactamente cuatro aplicaciones de A en B . Recordemos que todo elemento de A debe tener una y solo una imagen en B , por lo que las posibilidades están claras: f (1) = 2, f (2) = 2, g (1) = 3, g (2) = 3, h (1) = 2, h (2) = 3, y l (1) = 3, l (2) = 2 son todas las posibles funciones A → B . Tendríamos que f ( A ) = {2}, g ( A ) = {3}, h ( A ) = B y l ( A ) = B .
. (En estos ejemplos tendríamos que f (ℝ) = { a ∈ ℝ | a ≥ 1}, g (ℝ) = [−1, 1] y h (ℝ × ℝ) = { a ∈ ℝ | a ≥ 0}). Pero quizá el lector está menos acostumbrado a tratar con funciones sobre otros conjuntos, especialmente finitos. Por ejemplo, si A = {1, 2} y B = {2, 3} hay exactamente cuatro aplicaciones de A en B . Recordemos que todo elemento de A debe tener una y solo una imagen en B , por lo que las posibilidades están claras: f (1) = 2, f (2) = 2, g (1) = 3, g (2) = 3, h (1) = 2, h (2) = 3, y l (1) = 3, l (2) = 2 son todas las posibles funciones A → B . Tendríamos que f ( A ) = {2}, g ( A ) = {3}, h ( A ) = B y l ( A ) = B .
Ejercicio 1.1 Sean A y B conjuntos. Sea B Ael conjunto de las aplicaciones de A en B. Si A tiene n elementos y B tiene m elementos , probar que B Atiene m nelementos .
Dos funciones f : A → B , g : C → D son igualessi A = C , B = D y f ( a ) = g ( a ) para todo a ∈ A . Por ejemplo, las funciones f : ℤ → ℤ y g : ℤ → ℕ dadas por f ( z ) = g ( z ) = z 2no son iguales porque sus conjuntos finales son distintos.
Читать дальше


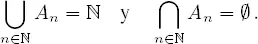
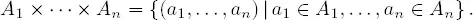
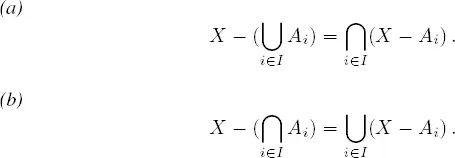

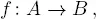
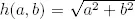 . (En estos ejemplos tendríamos que f (ℝ) = { a ∈ ℝ | a ≥ 1}, g (ℝ) = [−1, 1] y h (ℝ × ℝ) = { a ∈ ℝ | a ≥ 0}). Pero quizá el lector está menos acostumbrado a tratar con funciones sobre otros conjuntos, especialmente finitos. Por ejemplo, si A = {1, 2} y B = {2, 3} hay exactamente cuatro aplicaciones de A en B . Recordemos que todo elemento de A debe tener una y solo una imagen en B , por lo que las posibilidades están claras: f (1) = 2, f (2) = 2, g (1) = 3, g (2) = 3, h (1) = 2, h (2) = 3, y l (1) = 3, l (2) = 2 son todas las posibles funciones A → B . Tendríamos que f ( A ) = {2}, g ( A ) = {3}, h ( A ) = B y l ( A ) = B .
. (En estos ejemplos tendríamos que f (ℝ) = { a ∈ ℝ | a ≥ 1}, g (ℝ) = [−1, 1] y h (ℝ × ℝ) = { a ∈ ℝ | a ≥ 0}). Pero quizá el lector está menos acostumbrado a tratar con funciones sobre otros conjuntos, especialmente finitos. Por ejemplo, si A = {1, 2} y B = {2, 3} hay exactamente cuatro aplicaciones de A en B . Recordemos que todo elemento de A debe tener una y solo una imagen en B , por lo que las posibilidades están claras: f (1) = 2, f (2) = 2, g (1) = 3, g (2) = 3, h (1) = 2, h (2) = 3, y l (1) = 3, l (2) = 2 son todas las posibles funciones A → B . Tendríamos que f ( A ) = {2}, g ( A ) = {3}, h ( A ) = B y l ( A ) = B .










