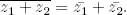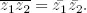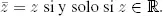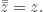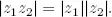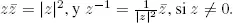17.Sea ℚ[ x ] el conjunto de los polinomios con coeficientes en ℚ.
(i) Probar que ℚ[ x ] es numerable.
(ii) Un número complejo α es algebraico sobreℚ si existe un polinomio 0 ≠ f con coeficientes en ℚ, tal que f ( α ) = 0. Utilizando que todo polinomio f de grado n tiene (como mucho) n ráıces complejas, probar que el conjunto de los números algebraicos es numerable.
( Ayuda: Para (i), agrupar los polinomios según grado y aplicar los problemas 1.16 y 1.14 (iv). Para (ii), volver a aplicar el problema 1.16).
18.Comprobar el siguiente argumento de D. Keyt para probar que ℝ no es numerable. Definimos una aplicación inyectiva f : P (ℕ) → [0, 1 / 9] de la manera siguiente. Si S ⊆ ℕ, entonces f ( S ) es el número real 0. a 0 a 1 a 2 … a n… , donde a n = 0 si n ∉ S , y a n = 1 si n ∈ S . Por ejemplo, f (∅) = 0, f (N) = 0.11111 … = 1 / 9, f ({0, 1, 3, 5}) = 0.110101, etc.
Utilizando los teoremas 1.8 y el problema 1.10, probar que [0, 1 / 9] no es numerable. Deducir que ℝ no es numerable.
19.Probar por inducción que
1 + 3 + 5 + … + (2 n − 1) = n 2.
20.Definimos 0! = 1 y n ! = 1 · 2 … ( n − 1) · n para n > 0. Si 0 ≤ a ≤ n , definimos
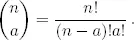
Si 1 ≤ a < n , probar que
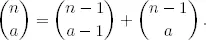
Deducir que
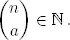
21.Probar que el producto de k naturales consecutivos es divisible por k !
22.( Binomio de Newton) Si a , b ∈ ℤ y n > 0, entonces
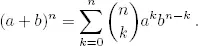
23.Sea p un primo, y sea 1 ≤ k < p . Probar que p divide a 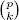 .
.
( Ayuda: Sabemos que p divide a 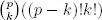 , pero p no puede dividir a ( p − k )! k !).
, pero p no puede dividir a ( p − k )! k !).
24.Probar las siguientes afirmaciones:
(i) Si n es impar, entonces n 2− 1 es divisible por 8.
(ii) Si a ≠ 0 es un entero, entonces a divide a (1 + a ) n− 1.
(iii) Si n es cualquier entero, entonces 4 no divide a n 2+ 2.
25.Si a , b , c son enteros no cero y mcd( a , c ) = 1, probar que mcd( a , b ) = mcd( a , bc ).
26.Recordar que si a ∈ ℝ − ℚ, entonces a se dice irracional.
(i) Sean a ∈ ℚ y b ∈ ℝ irracional. Probar que a + b es irracional. Si a ≠ 0, probar que ab es irracional.
(ii) Si n ∈ ℕ, probar que 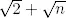 es irracional.
es irracional.
(iii) Probar que 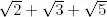 es irracional.
es irracional.
(iv) Probar que 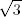 no se puede escribir de la forma
no se puede escribir de la forma 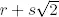 , donde r , s ∈ ℚ.
, donde r , s ∈ ℚ.
27.Comprobar que existen números irracionales a , b ∈ ℝ tales que a b es racional.
( Ayuda: Si 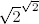 no es racional, volver a elevar a
no es racional, volver a elevar a 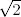 ).
).
28.Si z = a + bi , entonces el conjugado complejode z es 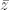 = a − bi . El módulode z es
= a − bi . El módulode z es 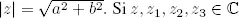 , probar lo siguiente:
, probar lo siguiente:
(i) z 1 z 2= z 2 z 1.
(ii) z 1( z 2 z 3) = ( z 1 z 2) z 3.
(iii) z 1( z 2+ z 3) = z 1 z 2+ z 1 z 3.
(iv) 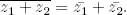
(v) 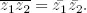
(vi) 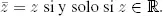
(vii) 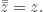
(viii) 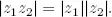
(ix) 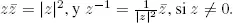
29.Hallar las ráıces 8-ésimas de la unidad.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

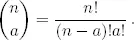
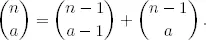
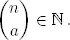
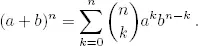
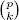 .
.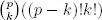 , pero p no puede dividir a ( p − k )! k !).
, pero p no puede dividir a ( p − k )! k !).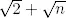 es irracional.
es irracional.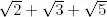 es irracional.
es irracional.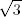 no se puede escribir de la forma
no se puede escribir de la forma 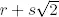 , donde r , s ∈ ℚ.
, donde r , s ∈ ℚ.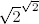 no es racional, volver a elevar a
no es racional, volver a elevar a 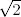 ).
).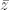 = a − bi . El módulode z es
= a − bi . El módulode z es 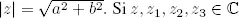 , probar lo siguiente:
, probar lo siguiente: