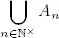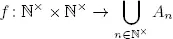Gabriel Navarro Ortega - Un curso de álgebra

4.Una aplicación f : X → Y es invertible izquierdasi existe g : Y → X tal que g ∘ f = 1 X. Se dice que f es invertible derechasi existe g : Y → X tal que f ∘ g = 1 Y. Probar que f es inyectiva si y solo si f es invertible a izquierda. Probar que f es suprayectiva si y solo si f es invertible a derecha.

( Nota: Para probar que si f es suprayectiva entonces f tiene inversa a derecha necesitamos el llamado axioma de elección . El axioma de elecciónafirma que si X es un conjunto cuyos elementos son conjuntos no vacíos, entonces es posible elegir un elemento de cada uno de esos conjuntos. Esto que parece algo obvio, no lo es. Por ejemplo, el axioma de elección es equivalente al teorema del buen orden que establece que cualquier conjunto posee una relación de orden tal que todo subconjunto no vacío tiene menor elemento. También es equivalente al llamado lema de Zorn , una de cuyas aplicaciones es que todo espacio vectorial tiene base. Nadie ha encontrado jamás explícitamente un buen orden en ℝ. En definitiva, todo matemático debe plantearse alguna vez si acepta el axioma de elección o no. Nuestro consejo es aceptarlo y seguir adelante).

5.Sean A y B conjuntos. Probar que existe f : A → B inyectiva si y solo si existe g : B → A suprayectiva.

( Ayuda: Aplicar el problema 1.4).

6.Sea f : A → B una aplicación. Probar:

(i) f es inyectiva si y solo si para todo par de aplicaciones h , g : X → A tales que f ∘ g = f ∘ h , entonces g = h .

(ii) f es suprajectiva si y solo si para todo par de aplicaciones h , g : B → X tales que g ∘ f = h ∘ f , entonces g = h .

7.Sean f : A → B y g : B → C aplicaciones biyectivas. Probar que

( g ∘ f ) −1= f − 1∘ g − 1.

( Nota: A veces este se denomina el Dressing-Undressing Principle , pues nos desvestimos en orden opuesto al que nos vestimos).

8.Sean f : A → B y g : C → D aplicaciones. Se define la aplicación producto f × g : A × C → B × D como ( f × g )(( x , y )) = ( f ( x ), g ( y )). Estudiar cuándo f × g es inyectiva o suprayectiva en función de f y de g .

9.Para cada una de las siguientes relaciones sobre ℤ probar si son relaciones de equivalencia y en caso afirmativo, describir las clases de equivalencia.

(i) R = {( x , y ) ∈ ℤ 2| x + y < 3}.

(ii) R = {( x , y ) ∈ ℤ 2| x + y es par}.

(iii) R = {( x , y ) ∈ ℤ 2| x = y o x = −y }.

(iv) R = {( x , y ) ∈ ℤ 2| y = x + 1}.

10.En el conjunto ℤ × ℤ ×, donde ℤ ×= ℤ − {0}, decimos que ( a , b ) y ( c , d ) están relacionados si ad = bc . Probar que esta relación es de equivalencia.

( Nota: Los números racionales se definen como las clases de equivalencia de esta relación).

11.Sea n > 0 un entero. Definimos la siguiente relación en ℤ. Decimos que a , b ∈ ℤ están relacionados si n divide a a − b . Probar que esta relación es de equivalencia y que la clase de equivalencia de a es

a + n ℤ = { a + nz | z ∈ ℤ}.

12.Probar que las siguientes aplicaciones son biyectivas:

(i) f : ℕ ×→ P = {2, 4, 6, …} y g : ℕ ×→ I = {1, 3, 5, …} dadas por f ( n ) = 2 n y g ( n ) = 2 n − 1. Concluir que el conjunto de números pares e impares positivos son numerables.

(ii) Si m ∈ ℕ ×, la aplicación f : ℕ ×→ { n ∈ ℕ ×| n > m } dada por f ( n ) = n + m .

(iii) f : ℕ ×→ ℤ dada por f ( n ) = n/ 2 si n es par, y f ( n ) = (1 − n ) / 2 si n es impar. Concluir que ℤ es numerable.

(iv) f : ℕ ×× ℕ ×→ ℕ ×dada por f ( n , m ) = 2 n−1(2 m − 1).

13.Si f : A → B es suprayectiva y A es numerable, entonces B es finito o numerable.

( Nota: Se pueden aplicar el problema 1.5 y el corolario 1.11. También podemos construir g : B → A inyectiva utilizando el teorema del buen orden en ℕ. Como A es numerable, entonces A está bien ordenado. Si b ∈ B , sea a el menor elemento de f − 1({ b }) y podemos definir g ( b ) = a ).

14.Sea A un conjunto numerable y sea B un conjunto. Probar las siguientes propiedades.

(i) Si B es finito, entonces A − B es numerable.

(ii) Si B es finito, entonces A ∪ B es numerable.

(iii) Si B es numerable, entonces A ∪ B es numerable. Concluir por inducción que la unión de un número finito de conjuntos numerables es numerable.

(iv) Si B es numerable, entonces A × B es numerable. Concluir por inducción que el producto cartesiano de un número finito de conjuntos numerables es numerable.

( Ayuda: Para (i), utilizar el teorema 1.10. Para (ii), podemos suponer por (i) que A ∩ B = ∅. Si B tiene m elementos, sabemos por el problema 1.12 (ii) que existe f : { n ∈ ℕ ×| n > m } → A biyectiva. Para (iii), por el mismo problema existen f : P → A y g : I → B biyectivas. Aplicar el problema 1.13. Para (iv), aplicar el problema 1.12 (iv)).

15.Probar que ℚ es numerable, utilizando que f : ℤ × ℤ ×→ ℚ, definida por f ( n , m ) = n/m , es suprayectiva.

16.Si A n es finito o numerable para todo n ∈ ℕ ×, probar que

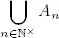
es finito o numerable.

( Ayuda: Por hipótesis, existe f n : ℕ ×→ A n suprayectiva. Definimos

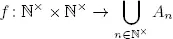
dada por f ( n , m ) = f n ( m ). Probar que f es suprayectiva).