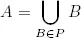( d) Si g ∘ f es suprayectiva , entonces g es suprayectiva .
Demostración.(a) Si g ( f ( a 1)) = g ( f ( a 2)), deducimos que f ( a 1) = f ( a 2) por ser g inyectiva. Por ser f inyectiva, tenemos que a 1= a 2.
(b) Si c ∈ C , entonces existe b ∈ B tal que g ( b ) = c , por ser g suprayectiva. Por ser f suprayectiva, existe a ∈ A tal que f ( a ) = b . Entonces g ( f ( a )) = c .
(c) Si f ( a 1) = f ( a 2), entonces g ( f ( a 1)) = g ( f ( a 2)). Como g ∘ f es inyectiva, deducimos que a 1= a 2.
(d) Si c ∈ C , por hipótesis existe a ∈ A tal que g ( f ( a )) = c . Si b = f ( a ), deducimos que g ( b ) = c 
Decimos que una función f : A → B es invertiblesi existe g : B → A tal que f ∘ g = 1 By g ∘ f = 1 A. Observamos que la función g , si existe, es única. Efectivamente, si h : B → A también satisface h ∘ f = 1 A, entonces
h = h ∘ 1 B= h ∘ ( f ∘ g ) = ( h ∘ f ) ∘ g = 1 A ∘ g = g .
La función g se llama la función inversade f y se escribe g = f − 1. Observamos que en este caso f − 1es también invertible y que ( f − 1) −1= f .
Teorema 1.4 Sea f : A → B. Entonces f es invertible si y solo si f es biyectiva .
Demostración.Supongamos que f es biyectiva. Construimos g : B → A de la siguiente manera. Dado b , sabemos que existe a ∈ A tal que f ( a ) = b , pues f es suprayectiva. Como f es inyectiva, a es único, y por tanto b unívocamente determina a . Definimos g ( b ) = a . Es inmediato que f ∘ g = 1 By g ∘ f = 1 A. Recíprocamente, supongamos que f es invertible y sea f − 1: B → A su inversa. Como f ∘ f − 1= 1 By f − 1 ∘ f = 1 Ason biyectivas, el teorema se sigue por el lema 1.3 partes (c) y (d). 
3
Si A es un conjunto, una relaciónen A es un subconjunto
R ⊆ A × A .
Decimos que a está relacionado con b si ( a , b ) ∈ R . Podemos pensar que una relación es sencillamente una función f : A × A → {sí, no}, donde R = {( a , b ) ∈ A × A | f ( a , b ) = sí}.
Por ejemplo, en el conjunto A = {1, 2, 3}, definimos la relación
R = {(1, 1), (1, 2), (3, 2)}.
En este caso, 1 está relacionado con 1 y con 2, 2 no está relacionado con ningún elemento, y 3 está relacionado con 2. Muchas veces, en lugar de especificar R , es más sencillo describir cuándo dos elementos están relacionados. Por ejemplo, en el conjunto A de los habitantes de una ciudad, podemos decir que dos elementos de A están relacionados si viven en el mismo edificio. En este caso, observamos que cualquier a ∈ A está relacionado consigo mismo, entre otras propiedades que analizamos a continuación. Necesitamos cierto lenguaje para hablar de relaciones.
Definición 1.5 Sea A un conjunto y R ⊆ A × A una relación en A .
(a) Decimos que R es reflexiva si ( a , a ) ∈ R para todo a ∈ A .
(b) Decimos que R es simétrica si siempre que ( a , b ) ∈ R , entonces ( b , a ) ∈ R .
(c) Decimos que R es antisimétrica si siempre que ( a , b ) ∈ R y ( b , a ) ∈ R , entonces a = b .
(d) Decimos que R es transitiva si siempre que ( a , b ), ( b , c ) ∈ R , entonces ( a , c ) ∈ R .
Muy pocas relaciones en un conjunto A son interesantes. De hecho, las relaciones interesantes son esencialmente de dos tipos. Una relación R es de equivalenciasi R es reflexiva, simétrica y transitiva. Una relación R es una relación de ordensi R es reflexiva, antisimétrica y transitiva.
Ejemplo 1.2
(a) En el conjunto ℝ de los números reales, definimos la relación ( a , b ) ∈ R si y solo si a ≤ b . Esta es una relación de orden.
(b) En el conjunto de habitantes de una ciudad, vivir en el mismo edificio establece una relación de equivalencia.
(c) En el plano ℝ 2, decimos que ( x 1, y 1) está relacionado con ( x 2, y 2) si se tiene que 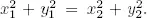 Esto define en el plano una relación de equivalencia.
Esto define en el plano una relación de equivalencia.
(d) Si f : A → B es una aplicación, definimos R = {( a 1, a 2) | f ( a 1) = f ( a 2)}. Entonces R es una relación de equivalencia.
(e) Si A es un conjunto, definimos una relación en el conjunto P ( A ) de todos los subconjuntos de A . Decimos que X e Y están relacionados si X ⊆ Y . Esto define una relación de orden en P ( A ).
Siempre que tengamos una relación de equivalencia R sobre un conjunto A , dicho conjunto queda partido en trozos disjuntos . (Dos conjuntos A y B son disjuntossi A ∩ B = ∅). Este es un hecho relevante. En el ejemplo 1.2 (b), los habitantes quedan distribuidos en edificios; en el ejemplo 1.2 (c), los elementos del plano quedan distribuidos en círculos de radio r para r ≥ 0. En general, cada elemento a ∈ A vive en su clase de equivalencia .
Una particiónde un conjunto A es un conjunto P de subconjuntos no vacíos de A tales que
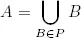
y B ∩ C = ∅ para todos B , C ∈ P distintos.
Читать дальше


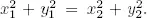 Esto define en el plano una relación de equivalencia.
Esto define en el plano una relación de equivalencia.