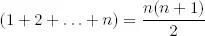Gabriel Navarro Ortega - Un curso de álgebra

A continuación probamos la unicidad de a . En efecto, si existiera otro elemento c ∈ A con la misma propiedad, tendríamos que a ≤ c y c ≤ a , con lo que a = c .

Al elemento a en el teorema 1.9 se le llama el menorelemento de A , y lo denotamos por min( A ).

Decimos que un conjunto A es numerablesi |ℕ ×| = | A |, donde ℕ ×= {1, 2, 3, …}. Algunos autores incluyen los conjuntos finitos entre los conjuntos numerables. Vemos que si A es numerable, entonces existe una aplicación biyectiva f : ℕ ×→ A , y así podemos escribir

A = { f (1), f (2), f (3), …}.

En definitiva, si A es numerable, entonces los elementos de A se pueden enumerar.

Teorema 1.10 Supongamos que A es un subconjunto infinito de ℕ. Entonces A es numerable .

Demostración.Como A no es vacío, sea a 1= min( A ). Como A − { a 1} no es vacío, sea a 2= min( A − { a 1}). En general, si tenemos definidos a 1, …, a k , como A − { a 1, …, a k } no es un conjunto vacío (pues A es infinito), podemos definir

a k +1= min( A − { a 1, …, a k })

para k ≥ 0. Observamos pues que tenemos definidos

a 1 < a 2 < … < a k< a k +1 < …

una cadena de elementos de A . Definimos f : ℕ ×→ A con f ( k ) = a k . Como a n< a m si n < m , observamos que f es inyectiva.

Probamos finalmente que f es suprayectiva. Sea a ∈ A . Sea B = { n ∈ A | n < a }. Si B = ∅, entonces a = a 1= f (1). En otro caso, B es un conjunto finito no vacío, que por tanto se puede escribir B = { a 1, …, a t } para algún t . Entonces a = a t +1= f ( t + 1), y el teorema queda probado.

Corolario 1.11 Si A es numerable y B ⊆ A , entonces B es finito o numerable .

Demostración.Supongamos que B es infinito. Sea f : A → ℕ ×una aplicación biyectiva. Aplicamos el teorema 1.10 al conjunto infinito f ( B ).

En los problemas guiaremos al lector sobre cómo probar que el conjunto de los números racionales es numerable, o que el de los números reales no lo es, entre otras propiedades.

5

El conjunto de los números enteroses

ℤ = {…, −n , …, −3, −2, −1, 0, 1, 2, 3, …, n , … | n ∈ ℕ}.

Suponemos que el lector está familiarizado con la suma y la multiplicación de números enteros. Es decir, en ℤ podemos sumar y multiplicar elementos: 2 + 3 = 5 o (−3)3 = −9. (Más adelante, diremos que ℤ con estas operaciones es un anillo ). También utilizamos que ℤ es un conjunto con un orden: 3 > 0, −5 ≤ 5 o 2 ≤ 2.

Estamos acostumbrados a dividir dos números enteros n y m , y obtener un dividendo d y un resto r . Este es el llamado algoritmo de división .

Teorema 1.12 (algoritmo de división) Sean n ∈ ℤ y 0 < m ∈ ℕ. Entonces existen dos únicos enteros d y r tales que n = dm + r con 0 ≤ r < m .

Demostración.Consideremos el conjunto A = { n−dm | d ∈ ℤ y n−dm ≥ 0}. Es decir, A está formado por los números naturales de la forma n − dm , con d ∈ ℤ. Si n ≥ 0, entonces n − ( −n ) m = n (1 + m ) ≥ 0, y deducimos que n (1 + m ) ∈ A . Si n ≤ 0, entonces n − nm = n (1 − m ) ≥ 0, y deducimos que n − nm ∈ A . En cualquier caso, concluimos que A ≠ ∅. Por el teorema 1.9, sea r el menor elemento de A . Como r ∈ A , entonces existe d ∈ ℤ tal que n − dm = r . Por tanto, n = dm + r . Si r ≥ m , tendríamos que

0 ≤ r − m = ( n − dm ) − m = n − ( d + 1) m ∈ A .

Pero r es el menor elemento de A y r − m < r . Esta contradicción prueba que r < m . Por tanto, hemos hallado d y r tales que n = dm + r con r < m .

Supongamos finalmente que d 1y 0 ≤ r 1 < m también satisfacen que n = d 1 m + r 1. Supongamos que r 1≥ r , por ejemplo. Como n = dm + r = d 1 m + r 1, tendremos que 0 ≤ r 1 − r = ( d − d 1) m ≤ r 1 < m . Necesariamente, d − d 1= 0 y por tanto r 1= r .

Vemos que el algoritmo de división es una consecuencia del teorema del buen orden en ℕ. Otra consecuencia de este es el llamado principio de inducción . En la práctica funciona así: Queremos probar que a partir de un cierto número natural k (habitualmente el 0 o el 1), todos los naturales mayores o iguales que k satisfacen una cierta propiedad. La estrategia que seguimos es la siguiente: primero probamos que k satisface la propiedad; y después probamos que si n ≥ k la satisface, entonces n + 1 también la satisface. El principio de inducción garantiza, entonces, que cualquier n ≥ k satisface la propiedad. En efecto, sea A el conjunto de números naturales mayores o iguales que k que satisfacen la propiedad, y sea B = { n ∈ ℕ | n ≥ k }. Queremos probar que A = B . Como A ⊆ B , en caso contrario tendríamos que

∅ ≠ B − A = { b ∈ B | b ∉ A } ⊆ ℕ.

Por el teorema del buen orden en ℕ, sea n el menor elemento de B − A . Notar que n > k , pues k ∈ A (ya que k satisface la propiedad). Entonces n − 1 no está en B − A , pues n es el menor elemento de B − A . Así, n − 1 ≥ k satisface la propiedad y por hipótesis también la satisface

n = ( n − 1) + 1.

Esta es la contradicción final.

Ejemplo 1.3Probamos que

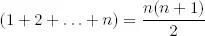
por inducción. Primero comprobamos que la igualdad es cierta para n = 1. Después suponemos que es cierta para n y la probamos para n + 1. Tenemos que