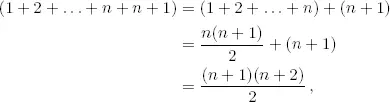
como queríamos probar.
El concepto fundamental en ℤ es la divisibilidad. Si a , b ∈ ℤ, con b ≠ 0, decimos que b dividea a si existe c ∈ ℤ tal que cb = a . A menudo se escribe b | a . En tal caso se dice que b es un divisorde a , y notamos que | c || b | = | a | (donde el valor absoluto| a | = a si a ≥ 0 y −a si a < 0). Si a ≠ 0, observamos que | b | ≤ | a |, por lo que concluimos que un entero a no cero solo tiene un número finito de divisores. Dados dos enteros n , m ∈ ℤ no cero, existe por tanto un mayor número natural 1 ≤ d que divide a ambos. Se dice que d es el máximo común divisorde n y m , y se escribe d = mcd( n , m ). Si d = 1, entonces n y m se dice que son coprimos.
Ejercicio 1.5 Si a divide a b y a c , probar que a divide a b + c. Si a divide a b , entonces a divide a bz para todo z ∈ ℤ.
Teorema 1.13 (máximo comú divisor) Sean n , m ∈ ℤ no cero , y sea d = mcd( n , m ).
(a) Entonces d es el menor elemento del conjunto
{ un + vm | u , v ∈ ℤ, un + vm > 0}.
En particular , existen enteros u , v ∈ ℤ tales que d = un + vm .
(b) Si e divide a n y a m , entonces e divide a d .
Demostración.Consideramos el conjunto
A = { un + vm | u , v ∈ ℤ, un + vm > 0},
que claramente no es vacío. (Por ejemplo, si n > 0 y m < 0, n + m 2∈ A ). Sea f = un + vm el menor elemento de A . Por el algoritmo de división, n = qf + r con 0 ≤ r < f . Entonces,
r = n − qf = n − q ( un + vm ) = (1 − qu ) n + ( −vq ) m .
Como r < f , esto solo puede ser cierto si r = 0. Deducimos que f divide a n y, análogamente, a m . En particular, f ≤ d , por definición de d . Como n = n 1 d , y m = m 1 d , tenemos que 0 < f = un 1 d + vm 1 d = ( un 1+ vm 1) d ≥ d , y concluimos que d = f .
Para la parte (b), si e divide a n y a m , por el ejercicio 1.1, concluimos que e divide a un + vm = d . 
Los números primos son fundamentales en matemáticas. Un número natural p > 1 es primosi no se puede escribir como p = ab , con a , b > 1. Es decir, si sus únicos divisores positivos son 1 y p . Observamos que si p es primo y n ∈ ℕ, entonces mcd( n , p ) = 1 o p , pues mcd( n , p ) es un divisor de p . Concluimos por tanto que o bien p divide a n o que p y n son coprimos.
Teorema 1.14 (Euclides) Sean n , m ∈ ℤ no cero .
(a) n y m son coprimos si y solo si existen u , v ∈ ℤ tales que un + vm = 1.
(b) Supongamos que n y m son coprimos. Si z ∈ ℤ, entonces n divide mz si y solo si n divide a z .
(c) Si p es primo , entonces p divide a nm si y solo si p divide a n o a m. En particular , si p divide a un producto de enteros n 1… n k , entonces p divide a algún ni .
Demostración.Si n y m son coprimos, ya sabemos que existen u , v ∈ ℤ tales que un + vm = 1, por el teorema 1.13 (a). Recíprocamente, si un + vm = 1, y d divide a n y a m , por el ejercicio 1.1, d divide a un + vm = 1, y esto completa el apartado (a).
En (b), supongamos que n divide a mz . Sabemos que 1 = un + vm para ciertos u , v ∈ ℤ, y que existe x ∈ ℤ tal que nx = mz . Ahora,
z = unz + vmz = unz + vnx = ( uz + vx ) n ,
y deducimos que n divide a z . La otra implicación es obvia.
Para probar el apartado (c), si suponemos que p divide a nm y que p no divide a n , tenemos que mcd( p , n ) = 1, y aplicamos el apartado (b). La segunda parte del apartado (c) se prueba fácilmente por inducción sobre k . 
Teorema 1.15 (teorema fundamental de la aritmética) Si n > 1 es un entero , entonces n se escribe de forma única como
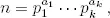
donde p 1 < … < p kson primos , y a 1, …, a kson números naturales no cero .
Demostración.Primero probamos la unicidad. Si 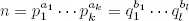 son dos expresiones como las del teorema, tenemos que p 1divide
son dos expresiones como las del teorema, tenemos que p 1divide  deducimos que p 1divide a cierto q i por el teorema 1.14 (c). Por tanto, p 1= q i , pues q i es primo. Por el mismo argumento, tenemos que q 1= p j para cierto j . Entonces q i = p 1≤ p j = q 1, por lo que deducimos que i = 1 y p 1= q 1. Utilizamos el mismo argumento para n/p 1.
deducimos que p 1divide a cierto q i por el teorema 1.14 (c). Por tanto, p 1= q i , pues q i es primo. Por el mismo argumento, tenemos que q 1= p j para cierto j . Entonces q i = p 1≤ p j = q 1, por lo que deducimos que i = 1 y p 1= q 1. Utilizamos el mismo argumento para n/p 1.
Para probar que cada n > 1 se escribe como producto de primos utilizamos inducción. Si n es primo, ya está. En caso, contrario, n = ab con a , b < n . Por inducción, a y b son producto de primos, y por tanto también lo es n . 
El conjunto de números racionaleses
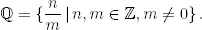
Suponemos que el lector está familiarizado con la suma y la multiplicación de números racionales, y sus propiedades más elementales. Por ejemplo, 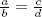 si y solo si ad = bc ,
si y solo si ad = bc ,
Читать дальше

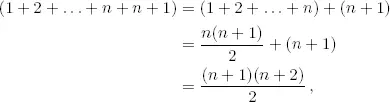

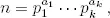
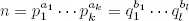 son dos expresiones como las del teorema, tenemos que p 1divide
son dos expresiones como las del teorema, tenemos que p 1divide  deducimos que p 1divide a cierto q i por el teorema 1.14 (c). Por tanto, p 1= q i , pues q i es primo. Por el mismo argumento, tenemos que q 1= p j para cierto j . Entonces q i = p 1≤ p j = q 1, por lo que deducimos que i = 1 y p 1= q 1. Utilizamos el mismo argumento para n/p 1.
deducimos que p 1divide a cierto q i por el teorema 1.14 (c). Por tanto, p 1= q i , pues q i es primo. Por el mismo argumento, tenemos que q 1= p j para cierto j . Entonces q i = p 1≤ p j = q 1, por lo que deducimos que i = 1 y p 1= q 1. Utilizamos el mismo argumento para n/p 1.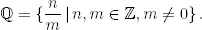
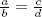 si y solo si ad = bc ,
si y solo si ad = bc ,










