Aufwachsen mit Anderen

Insgesamt hat die SNA eine Vielzahl weiterer hoch spezialisierter Indizes hervorgebracht (Hanneman & Riddle, 2011). Allein für die Quantifizierung von Segregation 3 in sozialen Netzwerken berichten Bojanowoski und Corten (2014) in einem Methodenreview neun verschiedene Indizes. Dennoch können Neuentwicklungen weiterer Indizes durchaus angezeigt sein (Zander et al., 2017). In einer jüngst veröffentlichten Studie zu bi- und monolingualen Lernenden konnten Henke, Zander und Baumert (2020) beispielsweise mithilfe eines solch neu entwickelten Indexes zeigen, dass unterschiedliche schulische Sprachsettings einen Einfluss auf die Tendenz der Lernenden haben, innerhalb bzw. außerhalb der eigenen Sprachgruppe nach Hilfe und fachlichem Austausch zu suchen. In Schulen, in denen eine bilinguale Sprachpraxis gefördert wurde (hier: Staatliche Europa-Schule Berlin), zählten vor allem die bilingual sozialisierten Lernenden zu den bevorzugten Hilfe- und Austauschpartnern und -partnerinnen ihrer Klasse. Ein gegenteiliges Bild ergab sich, wenn Deutsch die ausschließliche Schul- und Unterrichtssprache war: Hier zählten vor allem die monolingual deutschsprachig sozialisierten Lernenden zu den bevorzugten Hilfe- und Austauschpartnern und -partnerinnen der Klasse. Dieser Effekt war bei der Verwendung einfacher Degree-Maße, die sich auf alle Mitglieder im Netzwerk beziehen, nicht sichtbar.

Eine Frage, die sich bei der Betrachtung sozialer Netzwerkdaten typischerweise stellt, lautet, wie die beobachteten sozialen Strukturen innerhalb des Klassenzimmers mit bestimmten Merkmalen der Lernenden zusammenhängen. Die einfachste Form, um in einem sozialen Netzwerk Gruppen zu identifizieren, besteht darin, die erhobenen Netzwerkdaten mit Informationen zu weiteren Merkmalen der Lernenden zu verknüpfen, z. B. Geschlecht (vgl. Dijkstra & Berger, 2018) oder Sprachgruppenzugehörigkeit (vgl. Kindermann & Gest, 2018). Eine weitere, im Rahmen der Bildungsforschung bislang jedoch relativ selten genutzte Möglichkeit ist die Identifizierung von Gruppen aufgrund der Beziehungen, die die Personen untereinander haben (z. B. Grütter, Meyer & Glenz, 2014; Zander, Chen & Hannover, 2019). Diese Methode ist vor allem dann interessant, wenn Phänomene wie Selektion und Beeinflussung in Hinblick auf veränderbare Merkmale wie z. B. Einstellungen, Normen oder das Selbstkonzept untersucht werden sollen (Kindermann & Gest, 2018). Auch hier existiert eine Vielzahl von Prozeduren zur Identifikation existierender Gruppen in einem sozialen Netzwerk (Kindermann & Gest, 2018; van Duijn & Huisman, 2011). Bei den sogenannten Bottom-Up-Prozeduren (Hanneman & Riddle, 2011) wird innerhalb des Netzwerkes nach zuvor festgelegten Strukturen (z. B. Cliquen) gesucht (Wassermann & Faust, 1994). Da Personen in der Regel Mitglied mehrerer solcher Cliquen sind, ließe sich in einem Netzwerk beispielsweise auszählen, in wie vielen Vierer-Cliquen (n-Cliquen) – also Gruppen mit exakt vier Personen, die alle untereinander verbunden sind – eine Person inkludiert ist. Bei den sogenannten Bottom-Down-Prozeduren (ebd.) hingegen werden die Strukturmerkmale der Gruppen nicht zuvor rigide festgelegt, sondern ein statistisches Kriterium bestimmt, dem die Gruppenstruktur eines Netzwerkes genügen soll. Ein Beispiel für eine solche Prozedur bietet die Anwendung KliqueFinder (Frank, 1995, 1996). Der KliqueFinder-Algorithmus sucht nach einer Gruppenstruktur, in der die Wahrscheinlichkeit für eine Verbindung zwischen zwei Personen höher ist, wenn sie Mitglied derselben Gruppe sind, als wenn sie Mitglieder zweier unterschiedlicher Gruppen wären. Den von KliqueFinder aufgefundenen Gruppen müssen demnach keine sozialen Kategorien zugrunde liegen, wie z. B. das Geschlecht oder die Sprachzugehörigkeit. Ein Vorteil der Bottom-Down- gegenüber den Bottom-Up-Prozeduren ist, dass sie häufig Gruppenstrukturen aufdecken, die eine höhere Bedeutsamkeit für soziale Prozesse haben, als dies für mit Bottom-Up-Prozeduren identifizierte Gruppenstrukturen der Fall ist (van Duijn & Huisman, 2011).

Jede Darstellung eines sozialen Netzwerkes als Graph folgt dem Grundprinzip, dass Personen im Netzwerk als sogenannte Knoten und Beziehungen zwischen Personen als sogenannte Kanten betrachtet werden. Dabei repräsentieren einfache geometrische Formen wie Kreise, Dreiecke, Vierecke etc. diese Knoten. Kanten wiederum werden üblicherweise mit Linien (in ungerichteten Netzwerken) oder Pfeilen (in gerichteten Netzwerken) abgebildet. Durch die Wahl unterschiedlicher geometrischer Formen und Farben z. B. für Gruppen, aber auch einer Variation der Größe der Knoten, lassen sich so Strukturen in sozialen Netzwerken für die visuelle Anschauung aufdecken und herausarbeiten.

Ein vor allem in jüngeren Jahrgängen häufig beobachteter Effekt, der sich gut mithilfe von Visualisierungen aufzeigen lässt, ist die Präferenz von Mädchen und Jungen, mit Peers der eigenen Geschlechtsgruppe zu interagieren (Oerter & Montada, 2008, Kap. 8). An einem fiktiven Beispiel von Freundschaftswahlen in einer Schulklasse von 15 Lernenden lässt sich die sogenannte Geschlechtshomophilie 4 in sozialen Netzwerken gut erkennen: Mädchen und Jungen wählen ihre Freundschaften bevorzugt innerhalb der eigenen Geschlechtsgruppe, während Freundschaften außerhalb der eigenen Geschlechtsgruppe im Vergleich dazu eher selten sind ( Abb. 2.1).

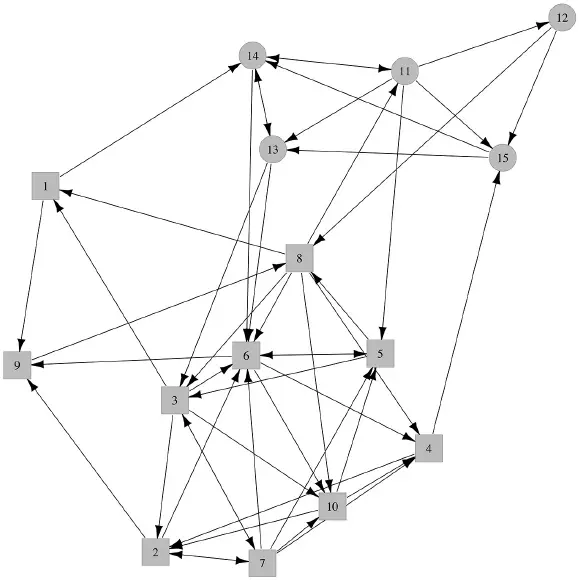
Abb. 2.1: Beispiel für die Visualisierung eines sozialen Netzwerkes als Graph, eigene Darstellung. Beispielhafte Darstellung einer Schulklasse, in der die Wahrscheinlichkeit einer Verbindung zwischen zwei Lernenden erhöht ist, wenn sie ein bestimmtes Merkmal (Geschlecht) teilen (Mädchen = Quadrate, Jungen = Kreise).

Neben den bereits beschriebenen deskriptiven Maßen (Indizes, Gruppen) verfügt die SNA über eine ebenso breite Palette an spezialisierten inferenzstatistischen Netzwerkmodellen (eine etwas ältere, aber konzise Darstellung hierzu findet sich z. B. bei van Duijn & Vermunt, 2006). Anders als die zuvor dargestellten Indizes haben diese Modelle das Ziel, das Entstehen bzw. die Entwicklung von Netzwerken mithilfe anderer Variablen zu erklären und diese Prozesse gegen den bloßen Zufall abzusichern. Weiterhin bieten sie die Möglichkeit, Effekte zu isolieren, indem sogenannte strukturelle Netzwerkeffekte 5 mitmodelliert werden und sich somit aus den anderen untersuchten Effekten herausrechnen lassen. Warum aber sind weithin gebräuchliche Verfahren, wie die Varianzanalyse, die lineare oder logistische Regression, für die Analyse von Netzwerken in der Regel nicht ausreichend? Ein Grund ist, dass im Fall von Netzwerken die übliche Annahme der bedingten Unabhängigkeit der Untersuchungseinheiten nicht mehr haltbar ist, da in der SNA explizit davon ausgegangen wird, dass Personen ihre Handlungen und Entscheidungen aneinander ausrichten und sich so potenziell auch gegenseitig in ihren Handlungen und Entscheidungen beeinflussen. Ignoriert man diesen Umstand bei der Untersuchung von sozialen Netzwerken, dann kann dies zu einer gravierenden Unter- oder Überschätzung anderer Parameter im Modell und damit zu Fehlinterpretationen führen (Lusher et al., 2013).