Bruno D´Amore - La Didáctica y la Dificultad en Matemática

1NRD Nucleo di Ricerca in Didattica (Núcleo de investigación en Didáctica).

Capítulo 1 Dificultades en matemática y en su aprendizaje

1.1. El sentido de la dificultad en matemática

La palabra «dificultad», un común pero difuso diccionario de la lengua italiana (el de Nicola Zingarelli, editado por Zanichelli en Bologna), la define cómo: «Cualidad de aquello que es difícil. Complicación, molestia, obstáculo, impedimento». La misma definición se encuentra en la enciclopedia Zanichelli.

Las definiciones tienen en común una cierta incoherencia entre un aspecto objetivo (dificultad, obstáculo) de la dificultad y uno más subjetivo («difícil», ¿para quién?, ¿respecto a qué?). Creemos que esta incoherencia reina soberana tanto en la visión popular de dificultad, como en la visión estrictamente escolar. Una materia es definida «difícil» sobre la base de la generalidad estadística de los resultados obtenidos, pero no existen caracterizaciones objetivas de esto (Fandiño Pinilla, 2006, lo demuestra ampliamente en el caso de la matemática).

Ahora, limitándonos a la dificultad en matemática, esta puede asumir por lo menos tres «sentidos» distintos, con referencia a nuestro interés:

• la dificultad en matemática del estudiante,

• la dificultad específica de algunos argumentos de la matemática,

• la dificultad del docente en la gestión de una situación matemática,

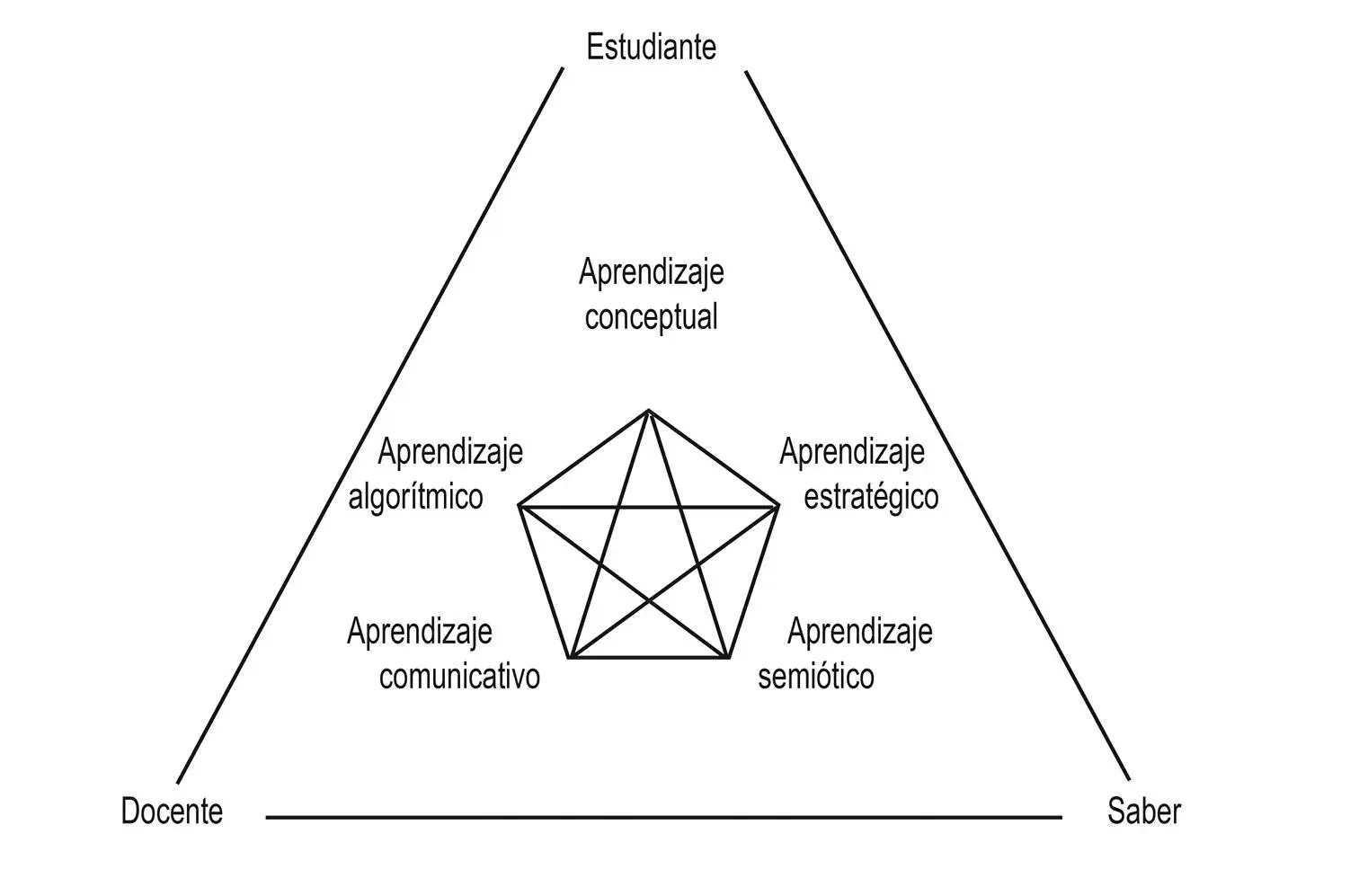
recalcando, más o menos en la misma dirección propuesta por Zan (2007), una estructura triangular que nos lleva mentalmente a considerar «el triángulo de la didáctica»: estudiante, docente, Saber (D’Amore 1999; para un análisis detallado de este esquema, véase: D’Amore, Fandiño Pinilla, 2002).

1.2. Especificidad de la dificultad en matemática

La dificultad en matemática puede ser analizada de forma mucho más específica, siguiendo una indicación que distingue varias componentes en el aprendizaje de la matemática (Fandiño Pinilla, 2005b). En efecto el aprendizaje de la matemática puede incluir diferentes tipos de aprendizajes:

• conceptual (noética);

• algorítmico (saber llevar a término una operación o secuencias compuestas de operaciones elementales, ...);

• estratégico (resolución de problemas, ...);

• comunicativo (argumentaciones, validaciones, demostraciones, ...);

• de la gestión de diversos registros semióticos.

Que las dificultades en estos particulares tipos de aprendizajes sean específicas está a la vista de todos: en efecto, hay estudiantes que han construido conceptos, pero no saben ejecutar algoritmos; estudiantes que llevan a término un algoritmo, pero no saben qué conceptos están a la base de dicha ejecución; estudiantes que han construido conceptos y saben ejecutar algoritmos, pero no saben resolver problemas; estudiantes que han construido conceptos, saben ejecutar algoritmos, saben resolver los problemas pero no saben comunicar aquello que han construido personalmente… y así sucesivamente; es por demás fácil hacer ejemplos para cada nivel escolar.

Por lo tanto, el estudio de las dificultades puede ser específico para cada una de los componentes del aprendizaje de la matemática. No obstante, algunas se entrelazan entre sí.

Efectivamente, pocos han sido los estudios específicos dedicados a la dificultad de la gestión de las diversas representaciones semióticas que el estudiante encuentra desde el primer día de clase (véase: D’Amore, 1998, 2000, 2002a, b, por ejemplo). En uno de estos trabajos (2002b) se da como hipótesis que una de las causas más difundidas del fracaso en el aprendizaje de la matemática es debida a la incapacidad de gestionar, al mismo tiempo, diversos registros semióticos y este hecho se confirma con numerosos ejemplos extraídos de la vida de aula.

Precisamente las especificidades en este campo fueron tomadas (a veces inconscientemente) como prototipos por algunos estudiosos en un pasado reciente, incluso sin distinciones notables.

Por ejemplo, la diferencia entre el «saber» (conceptual) y el «saber hacer» (un híbrido no bien definido, entre lo algorítmico y lo estratégico) viene tomado como específico de la dicotomía: aprendizaje de conocimientos y aprendizaje de competencias. Hoy en día esta visión tan simplista y banal ha sido totalmente superada (D’Amore, Godino, Fandiño Pinilla, 2008).

Volviendo a la terna enunciada en 1.1. sobre la dificultad específica de algunos argumentos de la matemática hay poco que decir.

Por ejemplo, construir el conocimiento del objeto matemático «propiedad conmutativa de la adición en N» tiene siempre un resultado positivo desde los primeros niveles de escolaridad; mientras que construir el conocimiento del objeto matemático «fracción» tiene casi siempre un resultado desastroso (y no sólo en los primeros niveles de escolaridad). Esto significa que existen obstáculos epistemológicos para el aprendizaje (de algunos temas) de la matemática; a este argumento notable dedicaremos todo el Capítulo 2 de este libro.

Por tanto, que existan en el estudiante dificultades objetivas en el aprendizaje de la matemática es aceptado por todos; algunas de éstas son de origen sensorial o físico o neurológico de carácter objetivo y evidenciadas, de las cuales vamos a ocuparnos brevemente en el parágrafo 1.4.; otras son más sutiles y, en nuestra opinión, están estrechamente relacionadas con las dificultades del docente en la gestión de una determinada situación matemática en el aula. Esto se debe a que algunos problemas se esconden entre los pliegues de la gramática de la comunicación (o, más en general, de la interacción) humana. A estos problemas dedicamos unos párrafos de este Capítulo 1 y más adelante, con detalles más específicos, los Capítulos 3 y 4.

Pero hay dificultades mucho más difíciles de reconocer y de verificar, y que, por lo tanto, es más complejo remediar.

1.3. Dificultades ocultas en el aprendizaje de la matemática

A las dificultades más «sutiles» del aprendizaje de la matemática se han dedicado algunos de los más notables estudiosos de la materia.

Sólo para dar la idea de lo que se trata, nos limitaremos aquí a dos ejemplos.

Primer ejemplo.

Una de las dificultades más nefastas, revelada por Guy Brousseau, consiste en el hecho de que el docente se convence a sí mismo y convence a sus estudiantes de que lo que están haciendo en el aula es buena matemática aunque no lo sea en absoluto. Al pasar a otro nivel escolar, o la primera dificultad, o al cambiar de docente, esta situación revela las fallas que a la larga son insuperables. Para explicar de qué se trata recurrimos a un extenso pasaje de D’Amore (2007a):

«El docente propone a sus estudiantes un problema que él cree análogo a otro que había propuesto anteriormente, pero en el cual habían fracasado. Él espera que reconozcan la similitud y que utilicen las correcciones y las explicaciones que ha dado para reproducir el mismo método de resolución, a fin de afrontar con éxito la nueva situación. El docente recomienda encarecidamente a sus estudiantes que busquen y usen esta analogía. Este procedimiento es exitoso, tiene éxito desde el punto de vista del docente. Pero es, en realidad, un fraude epistemológico. El estudiante da una respuesta correcta, pero no porque él haya entendido la necesidad matemática o lógica a partir del enunciado, no porque haya “entendido y resuelto el problema”, no porque haya aprendido el objeto matemático, sino simplemente porque estableció una similitud con otro ejercicio, no ha hecho más que reproducir una situación hecha por otro. Lo que es aún peor, es que para el estudiante ésta era la solicitud del docente. Creerá haber comprendido la cuestión matemática en juego, mientras que no ha hecho otra cosa que interpretar una intención didáctica enunciada explícitamente por el docente y dar la respuesta esperada.