1 ...7 8 9 11 12 13 ...17 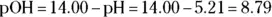
Now, if you have the pH or pOH, getting the corresponding 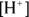 or
or 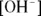 is a simple task:
is a simple task:
For example, a solution with a pH of 7.35 has a  .
.
Applying the Brønsted-Lowry theory
Because the acidity (pH) of the biological medium is so very important, in the following sections, we take a look at one of the most widely accepted theories concerning acids and bases — the Brønsted-Lowry theory. According to this theory, acids are proton  donors, and bases are proton acceptors.
donors, and bases are proton acceptors.
Swapping hydrogens between acids and bases
Acids increase the hydrogen ion concentration of a solution (they lower the pH, in other words). Some acids, known as strong acids, are very efficient at changing hydrogen ion concentration; they essentially completely ionize in water. Most acids — particularly biologically important acids — aren’t very efficient at generating hydrogen ions; they only partially ionize in water. These acids are known as weak acids.
Bases accept (react with), rather than donate, hydrogen ions in solutions. Bases decrease the hydrogen ion concentration in solutions because they react with these ions. Strong bases, although they can accept hydrogen ions very well, aren’t too important in biological systems. The majority of biologically important bases are weak bases.
 The Brønsted-Lowry theory helps to explain the behavior of acids and bases with respect to equilibrium. A Brønsted-Lowry acid is a hydrogen ion
The Brønsted-Lowry theory helps to explain the behavior of acids and bases with respect to equilibrium. A Brønsted-Lowry acid is a hydrogen ion  donor, and a Brønsted-Lowry base is a hydrogen ion acceptor. Acetic acid, a weak acid found in vinegar, partially ionizes in solution, evidenced by the following equation:
donor, and a Brønsted-Lowry base is a hydrogen ion acceptor. Acetic acid, a weak acid found in vinegar, partially ionizes in solution, evidenced by the following equation:
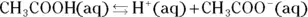
The double arrow indicates that the acetic acid doesn’t completely ionize. (For a strong acid, complete ionization would occur, indicated by a single arrow.) The equilibrium arrow 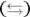 indicates that all three chemical species are present in the solution: the acetic acid, the acetate ion, and the hydrogen ion, along with the water solvent.
indicates that all three chemical species are present in the solution: the acetic acid, the acetate ion, and the hydrogen ion, along with the water solvent.
In the Brønsted-Lowry theory, you consider the acetate ion to be a base because it can accept a hydrogen ion to become acetic acid. According to this theory, two substances differing by only one hydrogen ion 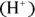 — such as acetic acid and the acetate ion — are members of a conjugate acid-base pair. The species with one additional hydrogen ion is the conjugate acid (CA), and the species with one less hydrogen ion is the conjugate base (CB).
— such as acetic acid and the acetate ion — are members of a conjugate acid-base pair. The species with one additional hydrogen ion is the conjugate acid (CA), and the species with one less hydrogen ion is the conjugate base (CB).
 You can express the equilibrium from the acetate example, like all equilibria, by using a mass-action expression — as long as a balance among the species is present. This expression is also known as a reaction quotient or an equilibrium constant. For acetic acid, this expression is as follows:
You can express the equilibrium from the acetate example, like all equilibria, by using a mass-action expression — as long as a balance among the species is present. This expression is also known as a reaction quotient or an equilibrium constant. For acetic acid, this expression is as follows:
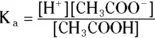
The a subscript means that this expression represents an acid. The square brackets refer to the molar equilibrium concentrations of the species present. You can express the K aas a pK a. The calculation of pK ais similar to the calculation of pH:
In terms of conjugate acids and bases, every K aexpression appears as
 No variations are allowed in this equation other than the actual formulas of the conjugate acid and base.
No variations are allowed in this equation other than the actual formulas of the conjugate acid and base.
Like an acid, a base has a K bvalue (the subscript b meaning base ). A weak base, like ammonia, is part of the following equilibrium:
The equilibrium constant expression for this equilibrium is

The generic form of a K bexpression is
As with a K aexpression, a K bexpression has no variations other than the actual formulas of the conjugate acid and base.
Every acid has a K a, and its corresponding conjugate base has a K b. The K aand the K bof a conjugate acid-base pair are related by the K w— the ionization constant for water. For a conjugate acid-base pair, 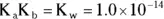 . In addition, you can use the following shortcut:
. In addition, you can use the following shortcut: 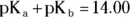 . (Are you enjoying this little bit of math? Biochemistry has a little more math than organic chemistry, but not nearly as much as general chemistry, so hang in there!)
. (Are you enjoying this little bit of math? Biochemistry has a little more math than organic chemistry, but not nearly as much as general chemistry, so hang in there!)
The K bfor the acetate ion, the conjugate base of acetic acid, would be associated with the following equilibrium expression:
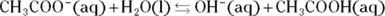
The K afor the ammonium ion, the conjugate acid of ammonia, would be associated with the following equilibrium expression:
Читать дальше

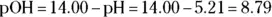
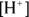 or
or 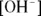 is a simple task:
is a simple task: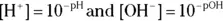
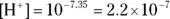 .
.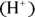 donors, and bases are proton acceptors.
donors, and bases are proton acceptors. The Brønsted-Lowry theory helps to explain the behavior of acids and bases with respect to equilibrium. A Brønsted-Lowry acid is a hydrogen ion
The Brønsted-Lowry theory helps to explain the behavior of acids and bases with respect to equilibrium. A Brønsted-Lowry acid is a hydrogen ion 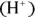 donor, and a Brønsted-Lowry base is a hydrogen ion acceptor. Acetic acid, a weak acid found in vinegar, partially ionizes in solution, evidenced by the following equation:
donor, and a Brønsted-Lowry base is a hydrogen ion acceptor. Acetic acid, a weak acid found in vinegar, partially ionizes in solution, evidenced by the following equation: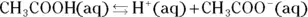
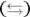 indicates that all three chemical species are present in the solution: the acetic acid, the acetate ion, and the hydrogen ion, along with the water solvent.
indicates that all three chemical species are present in the solution: the acetic acid, the acetate ion, and the hydrogen ion, along with the water solvent.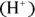 — such as acetic acid and the acetate ion — are members of a conjugate acid-base pair. The species with one additional hydrogen ion is the conjugate acid (CA), and the species with one less hydrogen ion is the conjugate base (CB).
— such as acetic acid and the acetate ion — are members of a conjugate acid-base pair. The species with one additional hydrogen ion is the conjugate acid (CA), and the species with one less hydrogen ion is the conjugate base (CB). You can express the equilibrium from the acetate example, like all equilibria, by using a mass-action expression — as long as a balance among the species is present. This expression is also known as a reaction quotient or an equilibrium constant. For acetic acid, this expression is as follows:
You can express the equilibrium from the acetate example, like all equilibria, by using a mass-action expression — as long as a balance among the species is present. This expression is also known as a reaction quotient or an equilibrium constant. For acetic acid, this expression is as follows: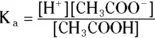
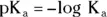
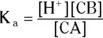

 . In addition, you can use the following shortcut:
. In addition, you can use the following shortcut:  . (Are you enjoying this little bit of math? Biochemistry has a little more math than organic chemistry, but not nearly as much as general chemistry, so hang in there!)
. (Are you enjoying this little bit of math? Biochemistry has a little more math than organic chemistry, but not nearly as much as general chemistry, so hang in there!)