Bruno D´Amore - Los problemas de matemática en la práctica didáctica

Por lo tanto, aceptando la posición de Heckhausen, se pude decir que el paso del deseo a la acción no es tan banal e inmediato6: hablar de motivación en general, entonces, resulta un poco vago; se necesita por lo menos un acto decisivo y este acto parece estar fuertemente influenciado por:

• las decisiones personales previas del estudiante

• la capacidad por parte del profesor de crear el contexto propicio.

Solo que el contexto en el cual se desarrolla la Matemática parece estar a menudo ya confeccionado; las expectativas del estudiante y las decisiones previas (del profesor) en este sentido parecen cristalizadas por un modelo matemático ya pre constituido, ya decidido a priori por alguien más o, lo que es aún peor, por la naturaleza misma de la asignatura.

Nos podríamos limitar a pensar en una situación estándar en la que el profesor

• adopta una estrategia para reforzar la motivación intrínseca, haciéndola lo más extrínseca posible; por ejemplo, la estrategia del incentivo (o, en líneas más generales, técnicas para aumentar la autoconfianza)

y, por lo tanto

• favorezca la creación de una motivación interna [el límite de todo esto es que parece casi inevitable recaer en un modelo preconcebido; ver: Franta (1993)].

• O, y es aquí donde entra en juego nuestra experiencia (la cual describiremos más adelante), se necesitaría:

• por un lado, desplazar la expectativa preconcebida en relación con la Matemática (estándar: la de la escuela); se trata sustancialmente de poner en cuestión las viejas convicciones;

• por otro lado, convencer implícitamente (para evitar la demagogia; es decir, basándose en la tarea asignada y no en recomendaciones ni prédicas estériles) que cualquiera está capacitado para construir Matemática (e incluso que la Matemática son un producto construible de manera personal); se trata entonces de elaborar nuevas convicciones;

• en fin, incluir en la evaluación (que frecuentemente es un paso motivacional fuerte para el estudiante) precisamente el fruto de las tareas asignadas, sin dar a la Matemática escolar tradicional un tratamiento diferente, en el momento de la evaluación, al de la Matemática construida sobre la instancia no estándar (de manera que se dé dignidad tanto a la parte estándar como a la no estándar); sustancialmente se trata de una elección de tipo didáctico con el fin de llevar a cabo los primeros dos puntos.

Se trata de crear un contexto emocional positivo que debe ser estable a nivel cognitivo y relacional (ver la experiencia narrada en D’Amore, Giovannoni, 1997).

En resumen, es obvio que la emoción que no se relaciona con hechos contingentes y raros modifica el sistema mismo de convicciones y valores (sobre este punto, ver Pellerery y Orio, 1996): las reacciones emocionales repetidas llevan a asumir comportamientos; nos parece que un resultado positivo se puede obtener si el estudiante está dispuesto a modificar el modelo mismo de expectativa estándar de la Matemática por un modelo no estándar que el profesor le da como alternativa (repetimos: no de manera episódica, sino de manera estable en cuanto al tiempo y a la motivación).

Lo anterior nos lleva necesariamente a una reflexión sobre los comportamientos frente a la Matemática.

Recuerdo aquí los estudios pioneros de Aiken (1970, 1976), en los cuales se distinguieron los momentos cruciales del nacimiento de un comportamiento negativo en relación con la Matemática en la franja escolar que corresponden a los grados de 6 hasta 8 (es decir más o menos alumnos entre los 11 y los 14 años de edad). Aquí se trata de revertir el fenómeno buscando, en la medida de lo posible, comportamientos positivos. Ahora bien, existe un Inventario de comportamientos con relación a la matemática de Sandman (1980) que incluye seis escalas de medida:

• el placer de hacer Matemática

• el valor dado a la Matemática

• la percepción del profesor de Matemática

• la ansiedad con respecto a la Matemática

• el auto concepto en el quehacer matemático

• la motivación para hacer Matemática.

El hecho que los valores mínimos se alcancen en el paso de la primaria a la escuela sucesiva, e incluso que tales valores se vuelvan negativos propiamente entre los grados 6 y 8, además de ser evidente ante los ojos de cualquier profesor e investigador, es confirmado por algunos estudios, por ejemplo los de Anderman y Maehr (1994); lo anterior se adhiere al rechazo, a la aversión, a la motivación negativa, al negarse a creer que la construcción personal de la Matemática es una posibilidad: una especie de autodefensa de un “monstruo” que no se puede controlar de ninguna manera.

El interés investigativo e incluso el interés solo pedagógico en este sentido se debe centrar, más que en los procesos de la enseñanza, en los procesos del aprendizaje; mejor aún, debe centrarse en la relación enseñanza/aprendizaje partiendo de las siguientes convicciones, tal como se presentan en D’Amore y Frabboni (1996):

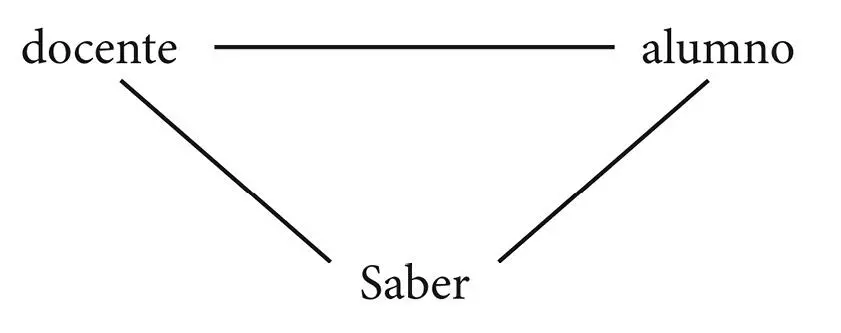
• el sujeto de la enseñanza de la Matemática no es la Matemática misma sino el alumno y, por lo tanto, la atención del profesor debe estar concentrada en los alumnos que están aprendiendo Matemática; de tal manera, se vuelve vital reconsiderar cada vez y tener siempre presentes todas las implicaciones incluidas en el triángulo de la Didáctica (Chevallard, 1985);

• el aprendizaje no se mide a través de una “cantidad de competencias adquiridas” vagas e indefinidas, se mide sobre todo a partir del placer, el deseo y la disposición a usarlas;

• la motivación intrínseca para aprender se debe mostrar como un objetivo didáctico, no como una condición de inicio (D’Amore, Sandri, 1994);

• en la enseñanza de la Matemática es necesario respetar al individuo; en este punto se sitúa la intención de no forzar aprendizajes vacíos o meramente formales, sino la necesidad de construir el pensamiento matemático, con la colaboración continua y cercana del alumno mismo, inclusive con la intención de dejar en él recuerdos positivos (no solo de orden cognitivo) de la materia (ver Furinghetti, 1993);

• en el proceso aprendizaje/enseñanza de la Matemática hay que considerar como algo prioritario que se debe tener siempre bajo observación la imagen que tanto el profesor como el alumno tienen de la Matemática, la imagen que tiene el alumno de sí mismo cuando hace Matemática y también la imagen que tiene el profesor de sí mismo en el desempeño de su rol.

Nota bibliográfica

Para la redacción de esta sección, hice uso de (Aiken, 1970, 1976; Anderman, Maehr, 1994; Boero, 1986; Bruner, 1961; Chevallard, 1985; Cornoldi, Caponi, 1997; D’Amore, 1994a, 1995a; D’Amore, Frabboni, 1996; D’Amore, Giovannoni, 1997; D’Amore, Martini, 1997b; D’Amore, Oliva, 1994; D’Amore, Sandri, 1994, 1996; Franta, 1993; Furinghetti, 1993; Hadamard, 1993; Hart, 1985; Heckhausen, 1990; Kruteskii, 1976; Kuhl, 1984; Laborde, 1982, 1995; Maier, 1993; Pellerey, 1992; Pellerey, Orio, 1996; Poincaré, 1906, 1914; Sandman, 1980; Zan, 1995, 1997).

De manera particular, sobre la distinción entre motivación y volición ver (D’Amore, 2003; D’Amore, Fandiño Pinilla, 2012; D’Amore, Godino, Arrigo, Fandiño Pinilla, 2003; Fandiño Pinilla, 2006; Pellerey, 1993).

A propósito de la motivación externa al aprendizaje de la Matemática, la educación de la intuición y la superación de los estereotipos escolares puede ser muy fructífero el estudio de las investigaciones de G. B. Saxe; quien, en efecto, hace mucho tiempo estudia situaciones de aprendizaje de la Matemática fuera del mundo escolar y, de tal manera, ha logrado comparar el aprendizaje escolarizado y el no escolarizado, obteniendo resultados interesantísimos. Sugiero (Saxe, 1977, 1979, 1982, 1985). Sobre todo, en lo relacionado con nuestro tema (Saxe, 1988). Para el lector poco familiarizado con las búsquedas bibliográficas (Saxe, 1991).