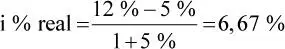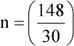Ejemplo 1.16
Calcular las tasas equivalentes a la TEA de 24 %.
Solución
| Tasa efectiva mensual: 12 meses |
|
|
| Tasa mensual = (1 + 24 %)^(1/12) – 1 |
= |
1,81 % |
| Tasa efectiva trimestral: 4 trimestres |
|
|
| Tasa trimestral = (1 + 24 %)^(1/4) – 1 |
= |
5,53 % |
| Tasa efectiva semestral: 2 semestres |
|
|
| Tasa semestral = (1 + 24 %)^(1/2) – 1 |
= |
11,36 % |
| Tasa efectiva diaria: 360 días |
|
|
| Tasa diaria = (1 + 24 %)^(1/360) – 1 |
= |
0,06 % |
Una tasa efectiva de 1,81 % mensual es equivalente a una tasa de 5,53 % efectiva trimestral, porque si se anualiza ambas tasas, dan idéntico resultado: 24 %. Lo mismo sucede con las otras tasas calculadas para el ejemplo 1.16. Es decir, una tasa de 0,06 % diaria es equivalente a una tasa de 11,36 % efectiva semestral o a una tasa de 1,81 % efectiva mensual.
1.3.4.2 Tasas proporcionales
Se dice que dos tasas son proporcionales si la tasa nominal subperiódica es igual a la tasa nominal dividida entre el número de periodos.
Ejemplo 1.17
Calcular las tasas proporcionales a la tasa nominal semestral de 12 %.
Solución
| Tasa nominal mensual: Un semestre tiene 6 meses |
| Tasa mensual = 12 % / 6 |
= |
2,00 % |
| Tasa nominal trimestral: Un semestre tiene 2 trimestres |
| Tasa trimestral = 12 % / 2 |
= |
6,00 % |
| Tasa nominal diaria: Un semestre tiene 180 días |
| Tasa diaria = 12 % / 180 |
= |
0,0667 % |
Es decir, una tasa nominal de 2 % mensual es proporcional a una tasa nominal trimestral de 6 % y proporcional a una tasa nominal semestral de 12 %.
Tasa de interés que considera el índice inflacionario. Esto significa que toma en cuenta la pérdida de valor del dinero a causa de la inflación.
La relación entre la tasa corriente y real se obtiene de la siguiente fórmula, que se verá con detalle en el capítulo 10.

Ejemplo 1.18
Calcular la tasa real sabiendo que un banco ofrece una tasa corriente de 12 % al año y el índice inflacionario anual se estima en 5 %.
Solución
Reemplazando:
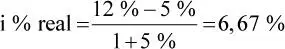
1.¿En cuánto tiempo se duplica una cantidad de dinero al 5 % de tasa de interés simple?
Solución
Llamemos a una cantidad de dinero: P.
Tasa de interés: 5 %
Periodos: n
Se utiliza la fórmula F = P + I y la fórmula de interés simple.
I = P × i % × n.
P + I = 2P
P + (P × i % × n) = 2P
P (1 + i % × n) = 2P
(1 + i % × n) = 2
Despejando P:
P = 20 periodos.
2.¿En cuánto tiempo se duplica una cantidad de dinero al 5 % de tasa de interés compuesto?
Solución
Llamemos a una cantidad de dinero: P.
Tasa de interés: 5 %
Periodos: n
Utilizando la fórmula F = P + I y la fórmula de interés compuesto.
I = P × [(1 + i) n– 1]
P + P × [(1 + i) n– 1] = 2P
P × (1 + i) n= 2P
(1 + i) n= 2
1,05 n= 2
Despejamos utilizando logaritmo de 2 en base 1,05. Nos da:
n = 14,2 periodos.
También se puede utilizar la función log en Excel.

Para el presente ejemplo: log(2;1,05) = 14,2 periodos
3.Asumiendo que la tasa de interés efectiva anual es 13 % capitalizable cada año, ¿cuál es la cantidad mínima de dinero que tendría que invertir por un periodo de tres años para ganar S/. 750 de interés?
Solución
Llamemos a una cantidad de dinero: P.
Tasa de interés efectiva: 13 % anual
I = S/. 750
n: 3 años
Utilizando la fórmula de I.
I = P × [ (1 + i) n– 1 ]
I = P × [(1 + 13 %) 3– 1] = S/. 750
Despejando P = S/. 1693,4.
Se requiere invertir S/. 1693,4 para obtener S/. 750 de interés luego de un año.
4.Usted quiere obtener S/. 51 000 de utilidad, con una rentabilidad de 2,5 % efectiva mensual. Si se considera que los años tienen 360 días, ¿cuánto tiempo deberá invertir?
a) 2 años
b) 9 trimestres
c) 148 días
Solución
Llamemos P a una cantidad de dinero.
Tasa de interés efectiva: 2,5 % mensual
I = S/. 51 000
Utilizando la siguiente fórmula de I = P × [ (1 + i) n– 1 ].
a) Periodo: 2 años
Como la tasa es mensual, n debe representar los 2 años, es decir,
n = 24 meses.
Utilizando la fórmula de I.
I = P × [(1 + i) n- 1]
I = P × [(1 + 2,5 %) 24– 1] = S/. 51 000
P = S/. 63 062,15
b) Periodo: 9 trimestres
Como la tasa es mensual, n debe representar los 9 trimestres. Esto significa que: n = 27 meses.
Utilizando la fórmula de I.
I = P × [(1 + i) n– 1]
I = P × [(1 + 2,5 %) 27– 1] = S/. 51 000
P = S/. 53 808,82
c) Periodo: 148 días
Como la tasa es mensual, n debe representar los 148 días, es decir, debe responder a la pregunta: ¿cuántos meses hay en 148 días?
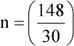
Utilizando la fórmula de I.
I = P × [(1 + i) n– 1]
I = P × [(1 + 2,5 %) (148/30)– 1] = S/. 51 000
P = S/. 393 678,75
5.¿Cuál es la tasa nominal trimestral capitalizable mensualmente si la tasa efectiva bimestral es 2 %?
Solución
Se pasa la tasa efectiva bimestral a tasa efectiva trimestral.
Tasa de interés efectiva trimestral = (1 + 2 %) (3/2)– 1 = 3,01 %
Para hallar la tasa nominal trimestral se utilizará la función tasa.nominal.
=TASA.NOMINAL(3,01%;3) = 2,99%
Son tres periodos de capitalización, dado que en un trimestre hay tres meses.
6.Hallar la tasa efectiva anual sabiendo que la tasa nominal es 7 % semestral capitalizable quincenalmente.
Solución
Utilizando la función Int.efectivo e ingresando como dato la tasa nominal semestral, se hallará la tasa efectiva semestral.
=INT.EFECTIVO(7%;12) = 7,23%
Se calcula la TEA:
TEA = (1 + 7,23 %) 2– 1 = 14,98 %
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.