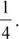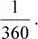Para realizar los cálculos matemáticos en ingeniería económica, vamos a utilizar la simbología convencional.
| P |
= |
capital inicial prestado o invertido |
| I |
= |
interés obtenido al final del periodo |
| i % |
= |
tasa de interés (o también llamado i pero se expresa en porcentaje) |
| n |
= |
número de periodos que dura la inversión o préstamo |
| F |
= |
valor futuro o valor total al finalizar los “n” periodos. Este valor contempla el capital inicial prestado o invertido (P) más el interés obtenido. Es decir: F = P + I |
| A |
= |
valor constante de una cuota o pago uniforme. Los flujos son ininterrumpidos e iguales en todos los periodos. |
En matemática financiera, el año base suele considerarse como un año ordinario de 360 días, con la finalidad de simplificar cálculos. Sin embargo, si tenemos las fechas exactas para determinar el interés exacto, se puede utilizar un año base de 365 días (o 366 en los años bisiestos).
Para la descripción de ambos tipos de interés (simple y compuesto) utilizaremos el interés a tasa vencida, es decir, cuando se paga al vencimiento.
Existe también interés pagado adelantado, tema perteneciente a las finanzas, que no se analizará en el presente acápite.
1.3.1 Interés simple e interés compuesto
Interés simple
Es el interés que se calcula sobre el capital original.
El monto de interés simple está dado por la siguiente fórmula:
I = C × i × n
Ejemplo 1.1
Determinar el interés anual de un préstamo de US$ 1000 a una tasa simple de 10 % anual.
Solución
Se realiza de la siguiente manera:
I = 1000 × 10 % × 1 = 100.
Ejemplo 1.2
Determinar el interés anual de un préstamo de US$ 1000 a una tasa simple de 5 % semestral.
Solución
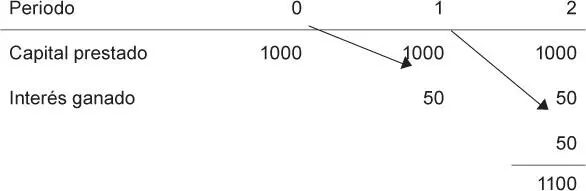
De esta forma:
I = 1000 × 5 % × 2 = 100
Como se puede apreciar, el interés generado es únicamente sobre el importe original del préstamo.
Ejemplo 1.3
Determinar el interés anual de un préstamo de US$ 1000 a una tasa simple de 2,5 % durante 45 días.
Solución
En este caso, 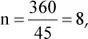 porque en un año de 360 días hay ocho periodos de 45 días.
porque en un año de 360 días hay ocho periodos de 45 días.
Aplicando la fórmula:
I = 1000 × 2,5 % × 8 = 200
En los tres ejercicios anteriores hemos calculado solo el importe del interés (I), pero ¿qué pasa si queremos determinar el valor final o valor futuro (F)? Para conseguirlo, utilizamos esta fórmula.
F = P × (1 + i × n)
Aplicando las fórmulas en los ejemplos 1.1, 1.2 y 1.3, tenemos:
• Valor final del ejemplo 1: F = 1000 × (1 + 10 % × 1) = 1100
• Valor final del ejemplo 2: F = 1000 × (1 + 5 % × 2) = 1100
• Valor final del ejemplo 3: F = 1000 × (1 + 2,5 % × 8) = 1200
Es aquel interés que se capitaliza, pasa a ser parte del capital principal y es base de cálculo para futuros intereses.
El valor futuro de un interés compuesto está dado por la siguiente fórmula:
F = P × (1 + i) n
Si queremos hallar únicamente el importe del interés, le descontamos el importe inicial.
I = F – P
Es decir, si queremos hallar únicamente el interés compuesto, se tiene:
I = P × (1 + i) n– P
I = P × [(1 + i) n– 1]
Ejemplo 1.4
Determinar el interés de un préstamo de US$ 100 a una tasa compuesta de 10 % anual durante 3 años.
Solución
De esta forma:
• Paso 1: hallar el importe final. Se aplica la fórmula.
F = 100 × (1 + 10 %) 3= 133,1
• Paso 2: restamos el importe inicial.
Interés = 133,1 – 100 = 33,1
Es decir, en 3 años se paga US$ 33,1 por concepto de interés.
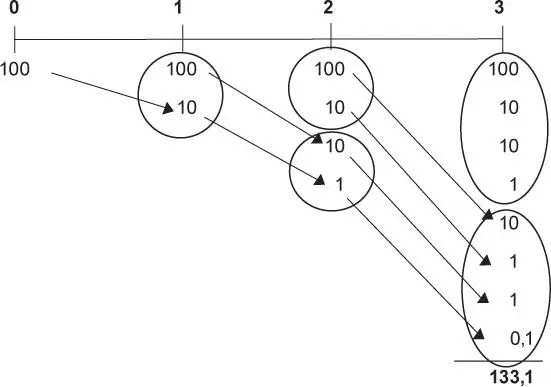
¿Cómo funciona el interés compuesto?
Tomando como base dicho ejemplo, se observa que inicialmente el préstamo es de US$ 100. Al finalizar el primer año y debido al interés, ya no se debe US$ 100, sino US$ 110 (US$ 100 × 10 %).
Como se puede ver, al finalizar el primer año se debe US$ 110, por lo que el interés acumulado al segundo año se calcula sobre US$ 110 y no sobre US$ 100, como en el interés simple. De esta manera, al cabo del segundo año el interés corresponde al 10 % de US$ 110, lo que nos da un total de US$ 121.
Para calcular el interés acumulado al finalizar el tercer año, calculamos el 10 % de US$ 121 (que es el saldo de lo que se debe al finalizar el segundo año), lo que nos da un total de US$ 133,1. Este es el importe total de la deuda al finalizar el tercer año.
Ejemplo 1.5
El señor Ortiz deposita un importe de $ 5000 en el banco, el cual le paga una tasa compuesta de 2 % anual. ¿Cuánto tendrá el Sr. Ortiz al finalizar el segundo año?
Solución
Aplicando la fórmula:
F = 5000 × (1 + 2 %) 2= US$ 5202
1.3.2 Interés nominal e interés efectivo
Interés nominal
La tasa de interés nominal es una tasa expresada en un solo periodo de tiempo y no considera la capitalización. Se basa en la tasa de interés simple.
En la conversión de la tasa nominal de un periodo a otro, dado que no consideramos capitalización, la conversión se hará mediante una multiplicación simple.
Tasa nominal 2= tasa nominal 1× n
Ejemplo 1.6
Si la tasa nominal semestral es 8 %, ¿cuánto será la tasa nominal anual?
Solución
Para pasarlo a anual, debemos calcular n. Si queremos pasar de semestral a anual, entonces sabemos que un año tiene dos semestres, por lo que el número de periodos sería 2. De esta manera, utilizamos la fórmula antes mencionada.
Tasa nominal anual = tasa nominal semestral × 2
Tasa nominal anual = 8 % × 2 = 16 %
Para calcular n se debe tener en cuenta los n periodos que presenta el periodo solicitado. Es decir:
• Si se quiere obtener la tasa anual y tenemos la tasa semestral, n sería 2.
• Si se busca la tasa anual y tenemos la tasa trimestral, n sería 4.
• Si se quiere calcular la tasa trimestral y tenemos la mensual, n sería 3.
• Si se quiere obtener la tasa trimestral y tenemos la tasa anual, n sería 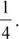
• Si se busca la tasa diaria y tenemos la tasa anual, n sería 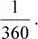
Ejemplo 1.7
Si la tasa nominal anual es 16 %, ¿cuánto será la tasa nominal trimestral?
Solución
Tasa nominal trimestral = tasa nominal anual × 
Читать дальше


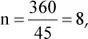 porque en un año de 360 días hay ocho periodos de 45 días.
porque en un año de 360 días hay ocho periodos de 45 días.