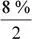Esto debido a que un año tiene cuatro trimestres.
Por tanto, la tasa nominal trimestral = 4 %.
La tasa de interés efectiva es la tasa aplicable a cierto periodo de tiempo, pero considera la capitalización. Se basa en la tasa de interés compuesta. Debido a que consideramos la capitalización, la conversión se hará mediante la siguiente fórmula:
tasa efectiva 2= (1 + tasa efectiva 1) n– 1
Ejemplo 1.8
Si la tasa efectiva semestral es 8 %, ¿cuánto será la tasa efectiva anual?
Solución
En este caso n = 2, y aplicamos la fórmula.
Tasa efectiva 2= (1 + tasa efectiva 1) n– 1
Tasa efectiva anual = (1 + tasa efectiva semestral) 2– 1
Tasa efectiva anual = (1 + 8 %) 2– 1 = 16,64 %
Ejemplo 1.9
Si la tasa efectiva anual es 16 %, ¿cuál será la tasa efectiva trimestral?
Solución
Tasa efectiva trimestral = (1 + 16 %) 1/4– 1 = 3,78 %
Ejemplo 1.10
Un cliente ahorrista requiere que usted le ayude a calcular la tasa de interés efectiva anual, asumiendo que la tasa de interés que paga el Banco Mi Perú es 1,2 % efectiva mensual.
Solución

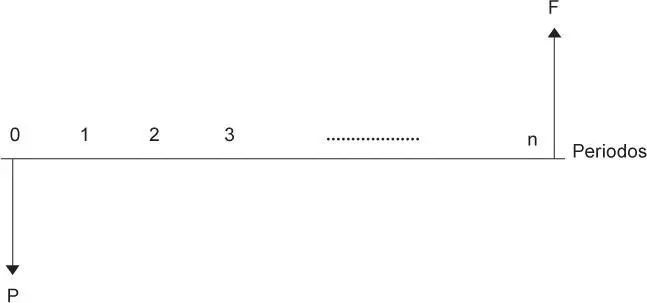
1.3.3 Relación entre la tasa nominal y la efectiva
La tasa nominal no se utiliza en las fórmulas de matemática financiera, pero es una forma de expresar la tasa efectiva.
Se sabe que:
| i % nominal por n periodos |
= |
(i % nominal por periodo) (n periodos) |
| i % efectiva por n periodos |
= |
( (1 + i % efectiva por periodo de capitalización)^n) – 1 |
Donde ^ es el símbolo de potencia.
1.3.3.1 Método para pasar de una tasa nominal a una efectiva
Para hallar una tasa efectiva a partir de una tasa nominal, debemos dividir la tasa nominal entre el número de periodos de capitalización respectivo.
De esta forma:

El método también se puede desarrollar a través de Excel. En este caso se presenta la función INT.EFECTIVO; si se conoce la tasa nominal y los periodos de capitalización, se devuelve la tasa efectiva:
INT.EFECTIVO(tasa_nominal;num_per_año).
Esta función permite obtener la tasa de interés efectiva en el “mismo periodo” de la tasa de interés nominal. Es decir, si se utiliza la función INT.EFECTIVO y se ingresa como dato la tasa nominal anual, el resultado será la tasa de interés efectiva anual. En este caso los periodos de capitalización serán los considerados en 1 año.
Si se ingresa como dato la tasa nominal semestral, el resultado será la tasa de interés efectiva semestral. En este caso los periodos de capitalización serán los considerados en un semestre.
Ejemplo 1.11
Convertir una tasa de 12 % nominal anual capitalizable mensualmente a una tasa efectiva.
Solución
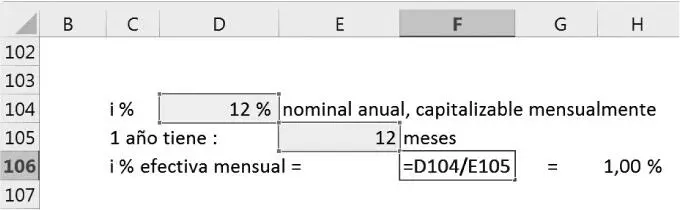
Si se utiliza la función INT.EFECTIVO, dará como resultado el interés efectivo anual si se ingresa la tasa de interés nominal anual.
| =INT.EFECTIVO(12%;12) |
|
| =12,68% |
tasa de interés efectiva anual |
Ejemplo 1.12
Convertir una tasa de 8 % nominal semestral, capitalizable trimestralmente a tasa efectiva.
Solución
i % = 8,00 % nominal semestral, capitalizable trimestralmente
1 semestre tiene: 2 trimestres
i % efectiva trimestral = 4,00 % = 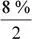
Si se utiliza la función INT.EFECTIVO, dará como resultado el interés efectivo semestral si se ingresa la tasa de interés nominal semestral.
| =INT.EFECTIVO(8%;2) |
|
| =8,16% |
Tasa de interés efectiva semestral |
Ejemplo 1.13
Convertir una tasa de 8 % nominal semestral, capitalizable quin cenalmente a tasa efectiva.
Solución
i % = 8,00 % nominal semestral, capitalizable quincenalmente
1 semestre tiene: 12 quincenas = 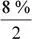
i % efectiva quincenal = 0,67 %
Si se utiliza la función INT.EFECTIVO, dará como resultado el interés efectivo semestral si se ingresa la tasa de interés nominal semestral y el periodo de capitalización quincenal.
| =INT.EFECTIVO(8%;12) |
|
| = 8,30% |
Tasa de interés efectiva semestral |
1.3.3.2 ¿Cómo pasar de una tasa efectiva a una nominal?
El Excel facilita el cálculo de la tasa nominal considerando la tasa efectiva y el número de periodos de capitalización. Lo permite mediante la función:
=TASA.NOMINAL (tasa_efect; num_per_año).
Esta función permite obtener la tasa de interés nominal en el “mismo periodo” de la tasa de interés efectiva. Es decir, si se utiliza la función TASA.NOMINAL y se ingresa como dato la tasa efectiva anual, el resultado será la tasa de interés nominal anual. En este caso, los periodos de capitalización serán los considerados en 1 año.
Si se ingresa como dato la tasa efectiva semestral, el resultado será la tasa de interés nominal semestral. En este caso, los periodos de capitalización serán los considerados en un semestre.
Ejemplo 1.14
Calcular la tasa nominal anual capitalizable mensualmente para una tasa efectiva anual de 18 %.
Solución
Según lo anterior, los periodos de capitalización en un año son 12, dado que 1 año tiene 12 meses

Ejemplo 1.15
Calcular la tasa nominal semestral capitalizable trimestralmente para una tasa efectiva anual de 18 %.
Solución
Dado que los datos deben tener la misma periodicidad del resultado, la tasa efectiva anual debe convertirse a efectiva semestral para utilizar la función Tasa.nominal.
Tasa efectiva semestral = (1 + 18 %) (1/2)–1 = 8,63 %
La tasa nominal semestral capitalizable trimestralmente se calculará:
=Tasa.nominal(8,63%;2) = 8,45%.
Tome en cuenta que el 8,63 % incluye sus respectivos decimales.
1.3.4 Tasas equivalentes y proporcionales
1.3.4.1 Tasas equivalentes
Se dice que dos tasas son equivalentes cuando operan en condiciones diferentes y dan el mismo resultado efectivo. Es decir, se trata de tasas que con diferente periodicidad, producen el mismo interés efectivo anual; normalmente se considera un año, pero puede compararse en otro periodo.
Читать дальше