In DIN 18801 [K12] Abschnitt 6.1.4 wird der Hinweis gegeben, dass auch Bauteile aus einem anderen Werkstoff als Stahl (z. B. Mauerwerkswände, Holzpfetten) zur Aussteifung von Stahlbauten herangezogen werden dürfen und diese dann ggf. auch für entsprechende Imperfektionen der auszusteifenden Bauwerksteile zu dimensionieren sind. Diese Regelung ist sicher auch auf eine Tragwerksberechnung nach EN 1993-1-1 zu übertragen.
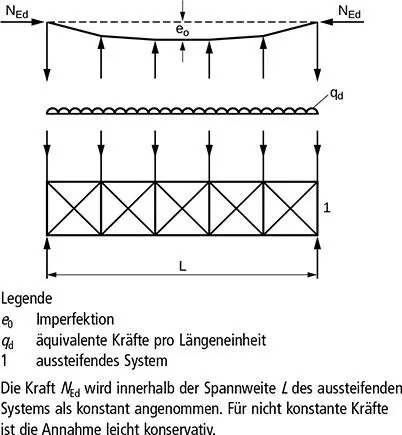
Bild 5.6. Äquivalente stabilisierende Ersatzkräfte
Anmerkung: δ qdarf 0 gesetzt werden, falls nach Theorie II. Ordnung gerechnet wird.
(3) Wird das aussteifende System zur Stabilisierung des druckbeanspruchten Flansches eines Trägers mit konstanter Höhe eingesetzt, kann die Kraft N Edin Bild 5.6wie folgt ermittelt werden:
(5.14) 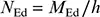
Dabei ist
| M Ed |
das maximale einwirkende Biegemoment des Trägers; |
| h |
die Gesamthöhe des Trägers. |
Anmerkung: Im Falle eines durch eine zusätzliche Drucknormalkraft beanspruchten Trägers enthält N Edauch einen Teil der Beanspruchung aus der einwirkenden Normalkraft.
(4) An Stößen von Trägern oder von druckbeanspruchten Bauteilen ist zusätzlich nachzuweisen, dass das aussteifende System eine am Stoßpunkt angreifende lokale Kraft von α m N Ed/100 von jedem Träger oder druckbeanspruchten Bauteil aufnehmen kann, welcher am gleichen Punkt gestoßen ist. Die Weiterleitung dieser Kräfte zu den nächsten Haltepunkten der Träger oder druckbeanspruchten Bauteile ist ebenfalls nachzuweisen, siehe Bild 5.7.
(5) Bei dem Nachweis der lokalen Kräfte nach (4) sind auch alle anderen äußeren Kräfte zu berücksichtigen, die auf das aussteifende System wirken, wobei die Kräfte aus dem Einfluss der Imperfektion aus (1) vernachlässigt werden dürfen.
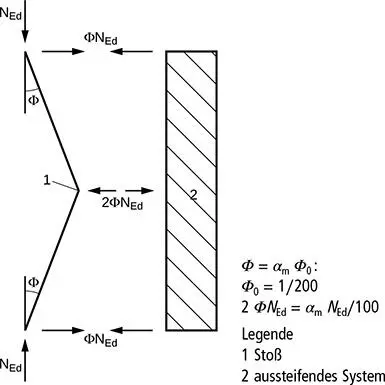
Bild 5.7. Lokale Ersatzkräfte an Stößen in druckbeanspruchten Bauteilen
5.3.4 Bauteilimperfektionen
(1) Die Einflüsse von Bauteilimperfektionen sind in den Gleichungen für die Stabilitätsnachweise von Bauteilen nach 6.3 enthalten.
(2) Wenn die Stabilitätsnachweise von Bauteilen nach Theorie II. Ordnung entsprechend 5.2.2(7) a) geführt werden, ist die Imperfektion für druckbeanspruchte Bauteile e 0in der Regel nach 5.3.2(3) b), 5.3.2(5) oder 5.3.2(6) zu berücksichtigen.
(3) Bei einem Biegedrillknicknachweis von biegebeanspruchten Bauteilen nach Theorie II. Ordnung darf die Imperfektion mit k · e 0angenommen werden, wobei e 0die äquivalente Vorkrümmung um die schwache Achse des betrachteten Profils ist. Im Allgemeinen braucht keine weitere Torsionsimperfektion betrachtet zu werden.
Anmerkung: Der Nationale Anhang kann den Wert von k festlegen. Der Wert von k = 0,5 wird empfohlen.
Zu 5.3.3(2)
Die Ersatzlast, wenn das aussteifende System sich nicht selbst auch verformt, kann durch die Umsetzung in eine äquivalente Gleichstreckenlast über die angenommene Parabelform gemäß Gl. (5.13)erfolgen. Daraus ergibt sich für e 0= α m⋅ L /500:
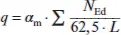
Diese Ersatzlasten gelten nur, wenn das aussteifende System sich nicht selbst auch verformt. δ qbeschreibt in Gleichung (5.13)die Verformung des aussteifenden Systems infolge der Imperfektion und weiterer äußerer Lasten. Wenn δ qausreichend klein ist, kann man diesen Effekt vernachlässigen. Hierfür gibt es in der Vornorm ENV 1993-1-1 [K45] das folgende Kriterium: δ q≤ L /2500.
zu 5.3.4(3) Anmerkung
Die Imperfektion ist anstelle von ( k · e 0) mit den Werten der Tabelle NA.3anzunehmen.
Diese Werte sind im Bereich 0,7 ≤ 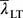 ≤ 1,3 zu verdoppeln .
≤ 1,3 zu verdoppeln .
Tabelle NA.3. Äquivalente Vorkrümmungen e 0/ L
| Querschnitt |
Abmessungen |
elastische Querschnittsausnutzung e 0/ L |
plastische Querschnittsausnutzung e 0/ L |
| gewalzte I-Profile |
h / b ≤ 2,0 |
1/500 |
1/400 |
|
h / b > 2,0 |
1/400 |
1/300 |
| geschweißte I-Profile |
h / b ≤ 2,0 |
1/400 |
1/300 |
|
h / b > 2,0 |
1/300 |
1/200 |
5.4 Berechnungsmethoden
5.4.1 Allgemeines
(1) Die Schnittgrößen können nach einer der beiden folgenden Methoden ermittelt werden:
a) elastische Tragwerksberechnung;
b) plastische Tragwerksberechnung.
Anmerkung: Zu Finite Element (FEM)-Berechnungen siehe EN 1993-1-5.
(2) Die elastische Tragwerksberechnung darf in allen Fällen angewendet werden.
(3) Eine plastische Tragwerksberechnung darf nur dann durchgeführt werden, wenn das Tragwerk über ausreichende Rotationskapazität an den Stellen verfügt, an denen sich die plastischen Gelenke bilden, sei es in Bauteilen oder in Anschlüssen.
An den Stellen plastischer Gelenke in Bauteilen sollte der Bauteilquerschnitt doppelt-symmetrisch oder einfach-symmetrisch mit einer Symmetrieebene in der Rotationsebene des plastischen Gelenkes sein und zusätzlich den in 5.6 festgelegten Anforderungen entsprechen. Tritt ein plastisches Gelenk an einem Anschluss auf, sollte der Anschluss entweder ausreichende Festigkeit haben, damit sich das plastische Gelenk im Bauteil bildet, oder er sollte seine plastische Festigkeit über eine ausreichende Rotation beibehalten können, siehe EN 1993-1-8.
(4) B Vereinfachend darf bei nach Elastizitätstheorie berechneten Durchlaufträgern eine begrenzte plastische Momentenumlagerung berücksichtigt werden, wenn die Stützmomente die plastische Momententragfähigkeit um weniger als 15 % überschreiten. Die überschreitenden Momentenspitzen müssen dann umgelagert werden, vorausgesetzt dass:
a) die Schnittgrößen des Tragwerks mit den äußeren Einwirkungen im Gleichgewicht stehen;
b) alle Bauteile, bei denen die Momente abgemindert werden, Querschnitte der Klasse 1 oder 2 (siehe 5.5) aufweisen;
c) Biegedrillknicken verhindert ist.
5.4.2 Elastische Tragwerksberechnung
(1) Bei einer elastischen Tragwerksberechnung ist in der Regel davon auszugehen, dass die Spannungs-Dehnungsbeziehung des Materials in jedem Spannungszustand linear verläuft.
Anmerkung: Bei der Wahl des Modells für verformbare Anschlüsse siehe 5.1.2.
Zu 5.3.4(3) und NDP
Die Imperfektionen für die Tragwerksberechnung nach Theorie II. Ordnung aus der Rahmenebene heraus, also für das Biegedrillknicken, sind abweichend von den ursprünglichen Empfehlungen nach EN 1993-1-1 gemäß der Tabelle NA.3anzunehmen. Im Gegensatz zum Biegeknicken, bei dem sich Stäbe mit großem h / b -Verhältnis günstiger verhalten als solche mit kleinem h / b - Verhältnis, ist es beim Biegedrillknicken anders. Beim Biegedrillknicken verhalten sich I-Profile mit h / b > 2,0 ungünstiger als solche mit h / b < 2,0. Untersuchungen haben gezeigt, dass die reduzierten Werte der Imperfektionen im mittleren Schlankheitsbereich (0,7 < 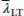 < 1,3) nicht angewendet werden dürfen, sondern zu verdoppeln sind, vgl. [K11, K28].
< 1,3) nicht angewendet werden dürfen, sondern zu verdoppeln sind, vgl. [K11, K28].
Читать дальше


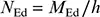

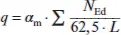
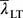 ≤ 1,3 zu verdoppeln .
≤ 1,3 zu verdoppeln .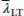 < 1,3) nicht angewendet werden dürfen, sondern zu verdoppeln sind, vgl. [K11, K28].
< 1,3) nicht angewendet werden dürfen, sondern zu verdoppeln sind, vgl. [K11, K28].










