Ulrike Kuhlmann - Stahlbau-Kalender 2022

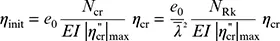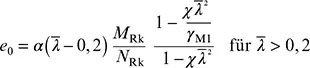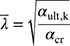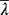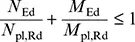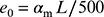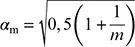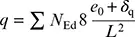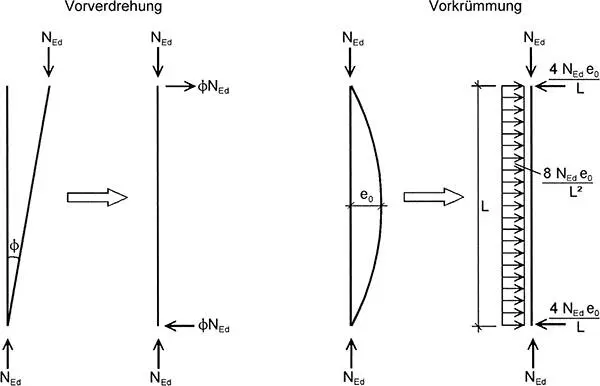
Bild 5.4. Ersatz der Vorverformungen durch äquivalente horizontale Ersatzlasten

(11) Alternativ zu (3) und (6) darf die Form der maßgebenden Eigenfigur η crfür das gesamte Tragwerk als Imperfektionsfigur angesetzt werden. Die maximale Amplitude dieser Imperfektionsfigur darf wie folgt ermittelt werden:

(5.9)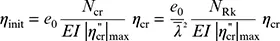

mit

(5.10)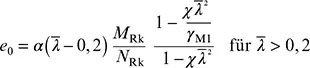

und

(5.11)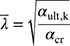

Dabei ist

	der Schlankheitsgrad des Tragwerks;
α	der Imperfektionsbeiwert der zutreffenden Knicklinie, siehe Tabelle 6.1und Tabelle 6.2;
χ	der Abminderungsfaktor der zutreffenden Knicklinie abhängig vom maßgebenden Querschnitt, siehe 6.3.1;
α ult,k	der kleinstmögliche Vergrößerungsfaktor der Normalkräfte N Edin den Bauteilen, um den chakteristischen Widerstand N Rkdes maximal beanspruchten Querschnitts zu erreichen, ohne jedoch das Knicken selbst zu berücksichtigen;
α cr	der kleinstmögliche Vergrößerungsfaktor der Normalkräfte N Ed, um ideale Verzweigungslast zu erreichen;
M Rk	die charakteristische Momententragfähigkeit des kritischen Querschnitts, z. B. M el,Rkoder M pl,Rk;
N Rk	die charakteristische Normalkrafttragfähigkeit des kritischen Querschnitts, z. B. N pl,Rk;
η cr	die Form der Knickfigur;
	das Biegemoment infolge η cram kritischen Querschnitt.

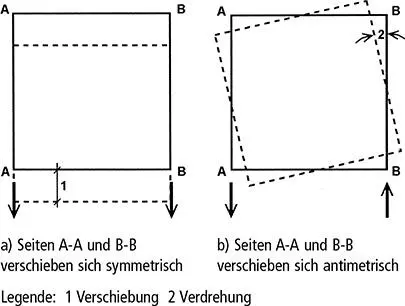
Bild 5.5. Verschiebungsmöglichkeiten und Einflüsse aus Torsion (Draufsicht)

Anmerkung 1: Für die Berechnung der Vergrößerungsfaktoren α ult,kund α crkann davon ausgegangen werden, dass die Bauteile des Tragwerks ausschließlich durch axiale Kräfte N Edbeansprucht werden. N Edsind dabei die nach Theorie I. Ordnung berechneten Kräfte für den betrachteten Lastfall. Biegemomente können vernachlässigt werden.

Für die elastische Tragwerksberechnung und plastische Querschnittsprüfung sollte die lineare Gleichung

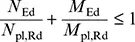
angewendet werden.

Anmerkung 2: Der Nationale Anhang kann Informationen zum Anwendungsbereich von (11) geben.

zu 5.3.2(11) Anmerkung 2

Das allgemeine Verfahren zur Ermittlung der maßgebenden Eigenfigur und deren maximale Amplitude der geometrischen Ersatzimperfektion darf angewendet werden. Falls unter Verwendung der nach Gleichung (5.9)ermittelten Imperfektionen die Ermittlung der Schnittgrößen des Gesamtsystems nach der Elastizitätstheorie erfolgt und ein Querschnittsnachweis unter Berücksichtigung der plastischen Tragfähigkeit geführt wird, dann muss der Querschnittsnachweis mit einer linearen Querschnittsinteraktion erfolgen.

(1) Bei der Berechnung aussteifender Systeme, die zur seitlichen Stabilisierung von Trägern oder druckbeanspruchter Bauteile benötigt werden, ist in der Regel der Einfluss der Imperfektionen der abgestützten Bauteile durch äquivalente geometrische Ersatzimperfektionen in Form von Vorkrümmungen zu berücksichtigen:

(5.12)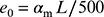

Dabei ist

L	die Spannweite des aussteifenden Systems;
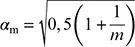	der Abminderungsfaktor;
m	die Anzahl der auszusteifenden Bauteile.

(2) Zur Vereinfachung darf der Einfluss der Vorkrümmung der durch das aussteifende System stabilisierten Bauteile durch äquivalente stabilisierende Ersatzkräfte nach Bild 5.6ersetzt werden:

(5.13)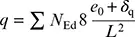

Dabei ist

Zu 5.3.2(11) mit NDP

Hier wird anstelle von auf die Stablänge bezogener pauschaler Schiefstellung und Vorkrümmung zusätzlich die Möglichkeit eröffnet, die maßgebende mit e 0skalierte Eigenform als Imperfektion anzusetzen. Der Ansatz der rechnerisch ermittelten Vorkrümmung e 0muss unter Berücksichtigung der Randbedingungen und somit der Schlankheit des betrachteten Systems erfolgen. Die Ermittlung der Imperfektionen aus der Eigenform wird z. B. im Leitfaden zum DIN-Fachbericht 103, Abs. II-X.4.3.2 bzw. Abs. 6.4.4 [K8] ausführlich beschrieben. Hinweise sind auch in [K5] gegeben. Der Nachweis darf so nur für elastische Tragwerksberechnung und lineare Querschnittsinteraktion geführt werden.

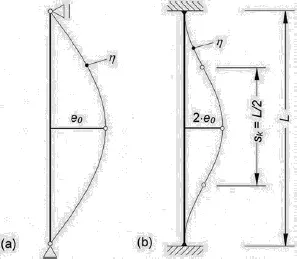
Bild K1. Ansatz der Imperfektionen bei einem gelenkig gelagerten Stab (a) und beidseitig eingespannten Stab (b) (nur qualitativer Vergleich)

In Bild K1ist beispielhaft der Ansatz bei einem gelenkigen und einem beidseitig eingespannten Stab dargestellt. Da sich die Vorkrümmung auf die Knicklänge bezieht ( Bild K1 (b)), ergibt sich bei dem beidseitig eingespannten Stab der Gesamtstich der Imperfektionsfigur zu η max= 2 · e 0. Es sei an dieser Stelle noch einmal darauf hingewiesen, dass e 0– anders als für den Pauschalansatz – hier von der Schlankheit des Systems abhängt und somit für die beiden dargestellten Fälle in Bild K1betragsmäßig unterschiedlich ist.

Zu 5.3.3

Leider erfolgt die Zuordnung von Stabilisierungskräften und Imperfektionen für aussteifende Tragwerksteile zu den verschiedenen Abschnitten in EN 1993-1-1, Kapitel 5.3 Imperfektionen nicht eindeutig. Grundsätzlich kann man unterscheiden zwischen vertikalen Aussteifungssystemen, die zum Beispiel in Form von vertikalen Fachwerkscheiben oder auch Massivwänden und Treppenhauskernen dafür sorgen, dass die übrige Stahl- bzw. Verbundrahmenkonstruktion als „unverschieblich“ charakterisiert werden kann, hierfür gilt 5.3.2(7) bis 5.3.2(10), und Horizontalaussteifungssysteme, die zum Beispiel als Dachverband bei Hallen sowohl Windlasten wie auch Abtriebskräfte zur Stabilisierung der Binder abtragen und in 5.3.3(1) bis 5.3.3(3) behandelt werden.